题目内容
如图,在直角坐标系中,O是原点,已知A(4,3),P是坐标轴上的一点,若以O,A,P三点组成的三角形为等腰三角形,则满足条件的点P共有 个,写出其中一个点P的坐标是 .


8;(5,0)(答案不唯一)
试题分析:如图所示,满足条件的点P有8个:
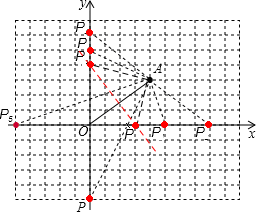
由A(4,3),根据勾股定理可得OA=5。
以O,A,P三点组成的三角形为等腰三角形分三种情况:
若OA=OP,则P的坐标为(5,0)或(0,5)或(﹣5,0)或(0,﹣5);
若OA=AP,则P的坐标为(8,0)或(0,6)。
若OP=AP,则P的坐标为(
 ,0)或(0,
,0)或(0, )。
)。综上所述,满足条件的点P有8个。

练习册系列答案
相关题目
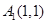 ,
,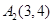 ,
,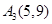
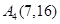 ,……,用你发现的规律确定
,……,用你发现的规律确定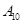 的坐标为
的坐标为 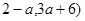 ,且点P到两坐标轴的距离相等,则点P的坐标为( )
,且点P到两坐标轴的距离相等,则点P的坐标为( )