题目内容
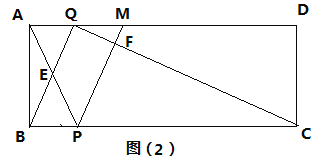
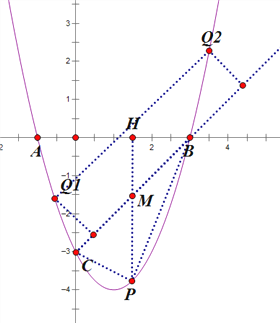
【题目】如图，抛物线y=x2+bx+c与x轴交于A、B两点，B点坐标为（3，0），与y轴交于点C（0，﹣3）
（1）求抛物线的解析式；
（2）点P在抛物线位于第四象限的部分上运动，当△BCP的面积最大时，求点P的坐标和△BCP的最大面积．
（3）当△BCP的面积最大时，在抛物线上是否点Q（异于点P），使△BCQ的面积等于△BCP，若存在，求出点Q的坐标，若不存在，请说明理由．
【答案】（1）y=x2﹣2x﹣3；（2）P点坐标为（
，﹣
）时，△BCP的面积最大，最大面积为
；（3）存在，Q点坐标为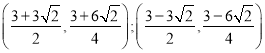
【解析】试题分析：（1）直接用代入法求函数的解析式；（2）连接BC，过点P作y轴的平行线，交BC于点M，交x轴于点H，求直线BC的函数解析式，设P点坐标为（x，x2﹣2x﹣3），则M点坐标为（x，x﹣3），则PM=x﹣3﹣（x2﹣2x﹣3）=﹣x2+3x，由S△PBC=
PM
OH+PM
HB=PM（OH+HB）=PM
OB=
PM，当PM有最大值时，△PBC的面积最大，由PM=﹣x2+3x＝－（x﹣）2+
可得，当x=时，有最大值PM=，则S△PBC=×=
,把x=代入 x2﹣2x﹣3＝﹣
，则点P的坐标为（
，﹣）；（3）求出直线Q1Q2的解析式，再求它与二次函数交点坐标即为所求；
试题解析：
(1）把B、C两点坐标代入抛物线解析式可得
，解得
，
∴抛物线解析式为y=x2﹣2x﹣3；
(2) 连接BC，过点P作y轴的平行线，交BC于点M，交x轴于点H，如图所示：
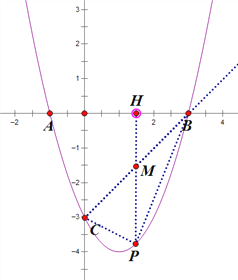
在y=x2﹣2x﹣3中，令y=0可得0=x2﹣2x﹣3，解得x=﹣1或x=3，则点B的坐标为（3，0），令x=0,y=-3,则点C的坐标为（0，－3），
∵B（3，0），C（0，﹣3），
∴直线BC解析式为y=x﹣3，
设P点坐标为（x，x2﹣2x﹣3），则M点坐标为（x，x﹣3），
∵P点在第四限，
∴PM=x﹣3﹣（x2﹣2x﹣3）=﹣x2+3x，
∴S△PBC=PM
OH+PM
HB=PM（OH+HB）=PM
OB=PM，
∴当PM有最大值时，△PBC的面积最大，
∵PM=﹣x2+3x=﹣（x﹣）2+，
∴当x=时，有最大值PM=，则S△PBC=×=，
此时P点坐标为（，﹣
）， S△PBC=，
即当P点坐标为（，﹣）时，△BCP的面积最大，最大面积为；
(3)∵△BCP的面积面积为
∴△BCP的高是
，
作直线BC的平行的直线Q1Q2，且距离直线BC为
，
∵直线BC的函数为y=x-3，
∴直线Q1Q2的解析式为y=x-
,
又∵二次函数的解析线为y=x2﹣2x﹣3，
∴两条直线交点Q2坐标为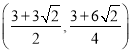
，Q1的坐标为
。
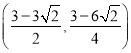∴存在，Q点坐标为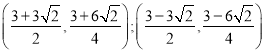
。
