Question

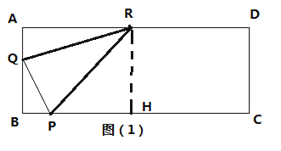
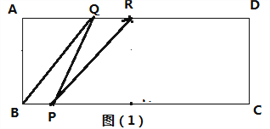
【题目】如图(1)，矩形ABCD，AB=2cm，AD=6cm，P、Q分别为两个动点，点P从B出发沿边BC运动，每秒1cm，点Q从B出发沿边B—C—D运动，每秒2cm.

（1）若P、Q两点同时出发，其中一点到达终点时另一点也随之停止，设△BPQ面积为S，时间为t秒，求S关于t的函数关系式及自变量的取值范围；

（2）若R为AD中点，连接RP、RQ，当以R、P、Q为顶点的三角形与△BPQ相似（含全等）时，求t的值；

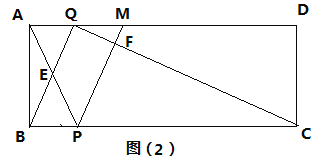
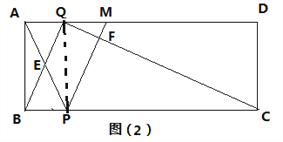
（3）如图（2）M为AD边上一点，AM=2，点Q在1.5秒时便停止运动，点P继续在BC上运动，AP与BQ交于点E，PM交CQ于点F，设四边形QEPF的面积为y，求y的最大值．

Answer 1

【答案】（1）， ；（2）t=0.25或；（3）

【解析】（1）根据矩形的对边相等表示出BC，然后表示出PB、QB，再根据三角形的面积列式整理即可得解，根据点Q先到达终点确定出x的取值范围即可；

（2）进行分类讨论求解即可；

（3）根据面积计算得出函数关系式，再求出最大值 即可.

试题解析：(1)

(2)当∠RQP=90时，△ARQ∽△BQP, ,AQ=1.5,BQ=0.5,t=0.25

当∠QPR=90时，△HPR∽△BQP, ,PH=4 不成立

当Q在AR上时，若QR=BP，则△RPQ全等于△BQP, ，

（3）连接PQ，则BP=t，则PC=6﹣x，

∵AM∥DP，

∴，

∴

∵S△APQ=ABAQ=t，

∴S△abe=，

同理可得，S△PQF=，

∴y=+=

当t=3时，上式等号成立，

∴y的最大值为： ．