题目内容
【题目】如图,在△ABC中,D是BC边的中点,分别过B、C做射线AD的垂线,垂足分别为E、F,连接BF、CE.
(1)求证:四边形BECF是平行四边形;
(2)我们知道S△ABD=S△ACD,若AF=FD,在不添加辅助线的条件下,直接写出与△ABD、△ACD面积相等的所有三角形.
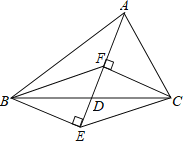
【答案】(1)详见解析;(2)与△ABD和△ACD面积相等的三角形有△CEF、△BEF、△BEC、△BFC.
【解析】
(1)根据全等三角形的判定和性质得出ED=FD,进而利用平行四边形的判定证明即可;
(2)利用三角形的面积解答即可.
(1)证明:在△ABF与△DEC中
∵D是BC中点,
∴BD=CD
∵BE⊥AE,CF⊥AE
∴∠BED=∠CFD=90![]() ,
,
在△ABF与△DEC中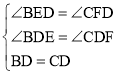 ,
,
∴△BED≌△CFD(AAS),
∴ED=FD,
∵BD=CD,
∴四边形BFEC是平行四边形;
(2)与△ABD和△ACD面积相等的三角形有△CEF、△BEF、△BEC、△BFC.
理由:∵四边形BECF是平行四边形,
∴S△BDF=S△BDE=S△CDE=S△CDF,
∵AF=DF,
∴S△ABF=S△BDF,S△ACF=S△CDF
∴S△BDF=S△BDE=S△CDE=S△CDF=S△ABF=S△ACF,
∴S△ABD=S△ACD=S△CEF=S△BEF=S△BEC=S△BFC.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目