题目内容
【题目】已知直线![]() 分别与
分别与![]() 轴交于
轴交于![]() 两点
两点
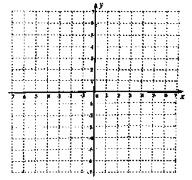
(1)求![]() 点的坐标,并在网格中用两点法画出直线
点的坐标,并在网格中用两点法画出直线![]() ;
;
(2)将直线![]() 向上平移6个单位后得到直线
向上平移6个单位后得到直线![]() ,画出平移后的直线
,画出平移后的直线![]() ,并直接写出直线
,并直接写出直线![]() 的函数解析式
的函数解析式
(3)设直线![]() 与
与![]() 轴交于点M,求
轴交于点M,求![]() 的面积.
的面积.
【答案】(1)(6, 0),(0,-3),见解析;(2)见解析,![]() ;(3)18
;(3)18
【解析】
(1)根据自变量与函数值的对应关系,即可得到答案;
(2)根据图象平移的规律:左加右减,上加下减,即可得到图象和解析式;
(3)把![]() 代入
代入![]() 求得M的坐标是(-6, 0),由点A、点B的坐标得到AM=12,BO=3,再根据三角形面积公式即可得到答案.
求得M的坐标是(-6, 0),由点A、点B的坐标得到AM=12,BO=3,再根据三角形面积公式即可得到答案.
解:(1)令![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() ,解得
,解得![]() ,
,
∴点A的坐标是(6, 0),点B的坐标是(0,-3).
直线![]() 如图所示
如图所示
(2)直线![]() 如图所示,直线
如图所示,直线![]() 的解析式为
的解析式为![]()
(3)把![]() 代入
代入![]() 得,
得,![]() ,解得
,解得![]() .
.
∴点M的坐标是(-6, 0),
∵点A的坐标是(6, 0),点B的坐标是(0,-3)
∴AM=6-(-6)=12,BO=3
∴S△MAB=![]()


练习册系列答案
相关题目
【题目】在平面直角坐标系中,横、纵坐标均为整数的点叫做整数点,设坐标轴的单位长度为1cm,整数点P从原点O出发,速度为1cm/s,且点P只能向上或向右运动,请回答下列问题:
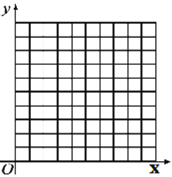
(1)填表:
点P从O点出发的时间 | 可以到达的整坐标 | 可以到达整数点的个数 |
1秒 | (0,1),(1,0) | 2 |
2秒 | (0,2),(2,0),(1,1) | 3 |
3秒 | ( ) | ( ) |
(2)当点P从点O出发10秒,可到达的整数点的个数是____________个;
(3)当点P从O点出发____________秒时,可得到整数点(10,5).