��Ŀ����
����Ŀ����1�������龳����ͼ1����ABC�ı�BC��ֱ��m�ϣ�AC��BC����AC=BC����EFP�ı�FPҲ��ֱ��m�ϣ���EF���AC�غϣ���EF=FP��
��ͼ1�У�AB��AP��������ϵ��_______��AB��AP��λ�ù�ϵ��_______
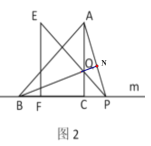
��2���������֣�����EFP��ֱ��m����ƽ�Ƶ�ͼ2��λ��ʱ��EP��AC�ڵ�Q������AP��BQ�����벢֤��BQ��AP��������ϵ��λ�ù�ϵ
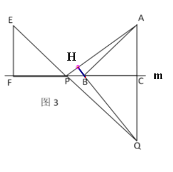
��3��������֤������EFP��ֱ��m����ƽ�Ƶ�ͼ3��λ��ʱ��EP���ӳ��߽�AC���ӳ����ڵ�Q������AP��BQ����2���еĽ��ۻ�������Ϊʲô��
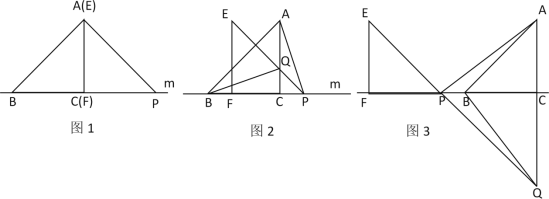
���𰸡���1����ȣ���ֱ��2����ȣ���ֱ,֤���ԣ�3������,֤����
��������
��1����˵����ABC���EFP��ȫ�ȵĵ���ֱ�������Σ�Ȼ����ݵ���ֱ�����ǵ����ʿɵ� ��BAC=��CAP=45�㣬��AB=AP���֡�BAP=90�㣬��AP��AB��
��2���ӳ�BQ��AP��H�㣬˵����QPCΪ����ֱ�������Σ�����QC=PC��Ȼ���ж���ACP�ա�BCQ����AP=BQ����BQC=��APC����������ֱ�������ε�����˵����PNB=90�㼴�ɣ�
��3������ͬ��2����֤BQ��AP�������������ϵΪ��ȣ�λ�ù�ϵΪ��ֱ��
�⣺��ͼ1��������ã�AC��BC��AC=BC��EF=AC��EF=FP��
���ABC���EFP��ȫ�ȵĵ���ֱ��������
���BAC=��CAP=45��
��AB=AP
�֡ߡ�BAP=��BAC����CAP= 90��
��AP��AB
�ʴ�ΪAB=AP��AP��AB��
��2��֤������ͼ���ӳ�BQ��AP��H�㣬
�ߡ�EPF=45
���CPQ=45��
��AC��BC.
���COP=��CPQ.
��CQ=CP������QPCΪ����ֱ��������
��Rt��BCQ��Rt��ACP��
BC=AC����BCQ=��ACP�� CQ=CP��
��Rt��BCQ��Rt��ACP��SAS��
��BQ=AP����BQC=��APC��
��Rt��BCQ����BQC+��PBN=90��
���APC+��PBN=90��
���PNB=90��
��QB��AP
��3������,�������£�
��ͼ3���ߡ�EPF=45
���CPQ=45��
��AC��BC.
���COP=��CPQ.
��CQ=CP������QPCΪ����ֱ��������
��Rt��BCQ��Rt��ACP��
BC=AC����BCQ=��ACP�� CQ=CP��
��Rt��BCQ��Rt��ACP��SAS��
��BQ=AP����BQC=��APC��
��Rt��BCQ����BQC+��CBQ=90��
�ߡ�PBH=��CBQ
���APC+��PBH=90��
���PHB=180��-����APC+��PBH��=90��
��QB��AP

 ����νӽ̲���ĩ���Ԥϰ�人������ϵ�д�
����νӽ̲���ĩ���Ԥϰ�人������ϵ�д� ������ҵ��ٳɳ����½������������ϵ�д�
������ҵ��ٳɳ����½������������ϵ�д�