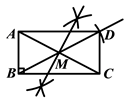题目内容
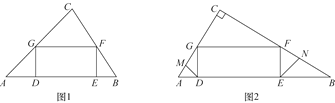
【题目】在面积为24的△ABC中,矩形DEFG的边DE在AB上运动,点F,G分别在边BC,AC上.
(1)若AB=8,DE=2EF,求GF的长;
(2)若![]() ,如图2,线段DM,EN分别为△ADG和△BEF的角平分线,求证:MG=NF;
,如图2,线段DM,EN分别为△ADG和△BEF的角平分线,求证:MG=NF;
(3)求出矩形DEFG的面积的最大值.
【答案】(1)GF的长为4.8;(2)证明见解析;(3)矩形DEFG的面积的最大值为12.
【解析】解:(1)∵△ABC的面积为24,AB=8,
∴△ABC边AB上的高h=6. 1分
设EF=x,则GF=DE=2x.
∵GF∥AB,∴△CGF∽△CAB,
∴![]() 即
即![]() 解得x=2.4. 3分
解得x=2.4. 3分
∴GF=4.8. 4分
(2)过点G作GP∥BC,过点D作DP∥EN,GP,DP交于点P,在DM的延长线上截取DQ=DP,连接QG.
∵DP∥EN,
∴![]()
又∵![]() ,∴
,∴![]() .
.
同理可得![]() .
.
又∵GD=FE,∴△GPD≌△FNE,∴![]() . 6分
. 6分
∵![]() ,∴△GQD≌△GPD,∴
,∴△GQD≌△GPD,∴![]() . 7分
. 7分
∵![]() ,∴
,∴![]() .
.
又∵![]() ,∴
,∴![]() . 9分
. 9分
∴MG=QG.
∴MG=NF. 10分
(3)作![]() 于点H,交GF于点I.
于点H,交GF于点I.
设AB=a,AB边上的高为h,DG=y,GF=x,则CH=h,CI=h-y,ah=48.
由(1)知,△CGF∽△CAB,
∴![]() 即
即![]()
则xh![]() 12分
12分
则矩形DEFG的面积![]() 即
即![]() .
.
由二次函数的有关性质知,当![]() 时,S取得最大值为
时,S取得最大值为![]() .
.
∴矩形DEFG的面积的最大值为12. 14分

练习册系列答案
相关题目