题目内容
【题目】如图(1)是一个长为 ![]() ,宽为
,宽为 ![]() (
( ![]() >
> ![]() )的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是.
)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是.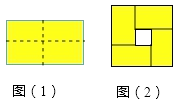
【答案】解:图(1)是一个长为2m,宽为2n(m>n)的长方形,
∴正方形的边长为:m+n,
∵由题意可得,正方形的边长为(m+n),正方形的面积为 ![]() ,
,
∵原矩形的面积为4mn,
∴中间空的部分的面积= ![]() -4mn=
-4mn= ![]() .
.
故答案为 ![]() .
.
【解析】根据图(1)与图(2)中黄色部分的面积相等,及图(2)正方形的边长,面积即可列出中间空的部分的面积的代数式。
【考点精析】掌握代数式求值是解答本题的根本,需要知道求代数式的值,一般是先将代数式化简,然后再将字母的取值代入;求代数式的值,有时求不出其字母的值,需要利用技巧,“整体”代入.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目