题目内容
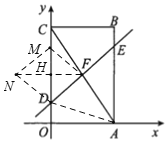
【题目】如图,矩形![]() 在平面直角坐标系中,
在平面直角坐标系中, ![]() ,
,![]() ,把矩形
,把矩形![]() 沿直线
沿直线![]() 对折使点
对折使点![]() 落在点
落在点![]() 处,直线
处,直线![]() 与
与![]() 的交点分别为
的交点分别为![]() ,点
,点![]() 在
在![]() 轴上,点
轴上,点![]() 在坐标平面内,若四边形
在坐标平面内,若四边形![]() 是菱形,则菱形
是菱形,则菱形![]() 的面积是( )
的面积是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
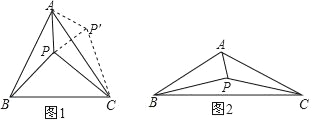
如图,连接AD,根据勾股定理先求出OC的长,然后根据折叠的性质以及勾股定理求出AD、DF的长,继而作出符合题意的菱形,分别求出菱形的两条对角线长,然后根据菱形的面积等于对角线积的一半进行求解即可.
如图,连接AD,
∵∠AOC=90°,AC=5,AO=3,
∴CO=![]() =4,
=4,
∵把矩形![]() 沿直线
沿直线![]() 对折使点
对折使点![]() 落在点
落在点![]() 处,
处,
∴∠AFD=90°,AD=CD,CF=AF=![]() ,
,
设AD=CD=m,则OD=4-m,
在Rt△AOD中,AD2=AO2+OD2,
∴m2=32+(4-m)2,
∴m=![]() ,
,
即AD=![]() ,
,
∴DF=![]() =
=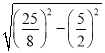 =
=![]() ,
,
如图,过点F作FH⊥OC,垂足为H,延长FH至点N,使HN=HF,在HC上截取HM=HD,则四边形MFDN即为符合条件的菱形,
由题意可知FH=![]() ,
,
∴FN=2FH=3,DH=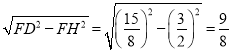 ,
,
∴DM=2DH=![]() ,
,
∴S菱形MFDN=![]() ,
,
故选C.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案
相关题目