Question

【题目】如图，CD⊥AB，EF⊥AB，垂足分别为D、F，∠1=∠2，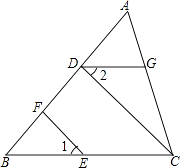

（1）试判断DG与BC的位置关系，并说明理由．
（2）若∠A=70°，∠BCG=40°，求∠AGD的度数．

Answer 1

【答案】
（1）

解：DG与BC平行．理由如下：

∵CD⊥AB，EF⊥AB，

∴CD∥EF，

∴∠1=∠BCD，

∵∠1=∠2，

∴∠2=∠BCD，

∴DG∥BC；

（2）

解：∵DG∥BC，

∴∠AGD=∠BCG=40°．

【解析】（1）根据在同一平面内，垂直于同条直线的两直线平行由CD⊥AB，EF⊥AB得到CD∥EF，根据平行线的性质得∠1=∠BCD，由于∠1=∠2，则∠2=∠BCD，然后根据内错角相等，两直线平行可判断DG∥BC；（2）根据平行线的性质由DG∥BC得到∠AGD=∠BCG=40°．