题目内容
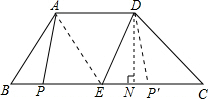
如图,在梯形ABCD中,AD∥BC,E是BC的中点,AD=5,BC=12,CD=4
,∠C=45°,点P是BC边上一动点,设PB的长为x.
(1)当x的值为______时,以点P、A、D、E为顶点的四边形为直角梯形;
(2)当x的值为______时,以点P、A、D、E为顶点的四边形为平行四边形;
(3)点P在BC边上运动的过程中,以P、A、D、E为顶点的四边形能否构成菱形?试说明理由.

| 2 |
(1)当x的值为______时,以点P、A、D、E为顶点的四边形为直角梯形;
(2)当x的值为______时,以点P、A、D、E为顶点的四边形为平行四边形;
(3)点P在BC边上运动的过程中,以P、A、D、E为顶点的四边形能否构成菱形?试说明理由.

(1)如图,分别过A、D作AM⊥BC于M,DN⊥CB于N,
则四边形AMND是矩形,
∴AM=DN,AD=MN=5,
而CD=4
,∠C=45°,
∴DN=CN=CD•sin∠C=4
×
=4=AM,
∴BM=CB-CN-MN=3,
若点P、A、D、E为顶点的四边形为直角梯形,
则∠APC=90°或∠DEB=90°,
当∠APC=90°时,
∴P与M重合,
∴BP=BM=3;
当∠DPB=90°时,P与N重合,
∴BP=BN=8;
故当x的值为3或8时,以点P、A、D、E为顶点的四边形为直角梯形;
(2)若以点P、A、D、E为顶点的四边形为平行四边形,那么AD=PE,
有两种情况:①当P在E的左边,
∵E是BC的中点,
∴BE=6,
∴BP=BE-PE=6-5=1;
②当P在E的右边,
BP=BE+PE=6+5=11;
故当x的值为1或11时,以点P、A、D、E为顶点的四边形为平行四边形;
(3)由(2)知,①当BP=1时,此时CN=DN=4,NE=6-4=2,
∴DE=
=
=2
≠AD,故不能构成菱形.
②当BP′=11时,以点P′、A、D、E为顶点的四边形是平行四边形
∴EP′=AD=5,
过D作DN⊥BC于N,
∵CD=4
,∠C=45°,
则DN=CN=4,
∴NP′=BP′-BN=BP′-(BC-CN)=11-12+4=3.
∴DP′=
=
=5,
∴EP′=DP′,
故此时?P′DAE是菱形.
即以点P、A、D、E为顶点的四边形能构成菱形;

则四边形AMND是矩形,
∴AM=DN,AD=MN=5,
而CD=4
| 2 |
∴DN=CN=CD•sin∠C=4
| 2 |
| ||
| 2 |
∴BM=CB-CN-MN=3,
若点P、A、D、E为顶点的四边形为直角梯形,
则∠APC=90°或∠DEB=90°,
当∠APC=90°时,
∴P与M重合,
∴BP=BM=3;
当∠DPB=90°时,P与N重合,
∴BP=BN=8;
故当x的值为3或8时,以点P、A、D、E为顶点的四边形为直角梯形;
(2)若以点P、A、D、E为顶点的四边形为平行四边形,那么AD=PE,
有两种情况:①当P在E的左边,
∵E是BC的中点,
∴BE=6,
∴BP=BE-PE=6-5=1;
②当P在E的右边,
BP=BE+PE=6+5=11;
故当x的值为1或11时,以点P、A、D、E为顶点的四边形为平行四边形;
(3)由(2)知,①当BP=1时,此时CN=DN=4,NE=6-4=2,
∴DE=
| DN2+NE2 |
| 42+22 |
| 5 |
②当BP′=11时,以点P′、A、D、E为顶点的四边形是平行四边形
∴EP′=AD=5,
过D作DN⊥BC于N,
∵CD=4
| 2 |
则DN=CN=4,
∴NP′=BP′-BN=BP′-(BC-CN)=11-12+4=3.
∴DP′=
| DN2+NP2 |
| 42+32 |
∴EP′=DP′,
故此时?P′DAE是菱形.
即以点P、A、D、E为顶点的四边形能构成菱形;



练习册系列答案
相关题目

 ,点E、F、G分别是线段BC、PC、BP的中点.
,点E、F、G分别是线段BC、PC、BP的中点.


 点B以3cm/s的速度运动.点P、Q分别从点A和点C同时出发,当其中一点到达端点时,另一点随之停止运动.
点B以3cm/s的速度运动.点P、Q分别从点A和点C同时出发,当其中一点到达端点时,另一点随之停止运动.