题目内容
【题目】如图,AC与BD相交于点O,AB∥CD,AB=CD,则图中的全等三角形共有( )
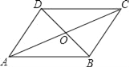
A. 1对B. 2对C. 3对D. 4对
【答案】D
【解析】
图中全等三角形有4对,是△ADB≌△CBD,△ABC≌△CDA,△AOD≌△COB,△AOB≌△COD.首先证明△AOB≌△COD(ASA),再利用全等三角形的性质和判定一一证明即可.
图中全等三角形有4对,是△ADB≌△CBD,△ABC≌△CDA,△AOD≌△COB,△AOB≌△COD,
理由是:∵AB∥CD,
∴∠ABD=∠CDB,∠BAO=∠DCO,
∵AB=CD,
∴△AOB≌△COD(ASA),
∴OA=OC,OB=OD,
∵∠AOD=∠COD,
∴△AOD≌△COB(SAS),
∴AD=BC,
∵AD=BC,CD=AB,AC=CA,
∴△ADC≌△CBA(SSS),
∵AD=BC,AB=CD,DB=BD,
∴△ADB≌△CBD(SSS),
故选:D.

练习册系列答案
相关题目


