题目内容
【题目】如图，在△ABC中，∠ABC=60°，BC=2，CD是△ABC的一条高线．若E，F分别是CD和BC上的动点，则BE+EF的最小值是_____．
【答案】
．
【解析】
作B关于CD的对称点B′，过B′作B′F⊥BC于F交CD于E，则B′F的长度即为BE+EF的最小值，根据直角三角形的性质得到BD=
CD，根据已知条件得到BB′=BC，推出△CDB≌△BB′F，于是得到B′F=CD．
作B关于CD的对称点B′，过B′作B′F⊥BC于F交CD于E，
则B′F的长度即为BE+EF的最小值，
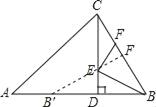
∵∠ABC=60°，CD⊥AB，
∴∠BCD=30°，
∴BD=CD，
∵BD=BB′，
∴BB′=BC，
在△CDB与△B′FB中，
，
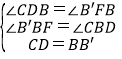∴△CDB≌△BB′F，（AAS）
∴B′F=CD=
BC=．
故答案是：．
练习册系列答案
相关题目
