题目内容
 如图,函数y=
如图,函数y=| k | x |
(1)若△ABD的面积为4,求点B的坐标;
(2)四边形ABCD能否成为平行四边形?若能,求点B的坐标,若不能说明理由;
(3)当AC=BD时,求证:四边形ABCD是等腰梯形.
分析:(1)将A的坐标代入反比例解析式中求出k的值,确定出反比例解析式,将B的坐标代入反比例解析式中,求出mn的值,三角形ABD的面积由BD为底边,AE为高,利用三角形面积公式来求,由B的坐标得到BD=m,由AC-EC表示出AE,由已知的面积,利用面积公式列出关系式,将mn的值代入,求出m的值,进而确定出n的值,即可得到B的坐标;
(2)假设四边形ABCD为平行四边形,利用平行四边形的性质得到BD与AC互相平分,得到E为AC的中点,E为BD的中点,由A的坐标求出E的坐标,进而确定出B的坐标,将B坐标代入反比例解析式检验,B在反比例图象上,故假设正确,四边形ABCD能为平行四边形;
(3)由由AC=BD,得到A的纵坐标与B的横坐标相等,确定出B的横坐标,将B横坐标代入反比例解析式中求出B的纵坐标,得到B的坐标,进而确定出E的坐标,得到DE=CE=1,由AC=BD,利用等式的性质得到AE=BE,进而得到两对对应边成比例,且由对顶角相等得到夹角相等,利用两边对应成比例且夹角相等的两三角形相似,得到三角形DEC与三角形AEB相似,由相似三角形的对应角相等得到一对内错角相等,利用内错角相等两直线平行得到CD与AB平行,而在直角三角形ADE与直角三角形BEC中,DE=EC,AE=BE,利用勾股定理得到AD=BC,且AD与BC不平行,可得出四边形ABCD为等腰梯形.
(2)假设四边形ABCD为平行四边形,利用平行四边形的性质得到BD与AC互相平分,得到E为AC的中点,E为BD的中点,由A的坐标求出E的坐标,进而确定出B的坐标,将B坐标代入反比例解析式检验,B在反比例图象上,故假设正确,四边形ABCD能为平行四边形;
(3)由由AC=BD,得到A的纵坐标与B的横坐标相等,确定出B的横坐标,将B横坐标代入反比例解析式中求出B的纵坐标,得到B的坐标,进而确定出E的坐标,得到DE=CE=1,由AC=BD,利用等式的性质得到AE=BE,进而得到两对对应边成比例,且由对顶角相等得到夹角相等,利用两边对应成比例且夹角相等的两三角形相似,得到三角形DEC与三角形AEB相似,由相似三角形的对应角相等得到一对内错角相等,利用内错角相等两直线平行得到CD与AB平行,而在直角三角形ADE与直角三角形BEC中,DE=EC,AE=BE,利用勾股定理得到AD=BC,且AD与BC不平行,可得出四边形ABCD为等腰梯形.
解答:解:(1)将A(1,4)代入反比例解析式得:4=
,即k=4,
∴反比例解析式为y=
,将B(m,n)代入得:mn=4,
∴BD=m,AE=AC-EC=4-n,
∵S△ABD=
AE•BD=
m(4-n)=4,
∴2m-
mn=2m-2=4,解得:m=3,
∴n=
,
则B(3,
);
(2)四边形ABCD能成为平行四边形.理由为:
若四边形ABCD为平行四边形,则AC、BD互相平分,即E为AC、BD的中点,
∵A(1,4),
∴E(1,2),B(2,2),
将x=2代入反比例解析式得:y=
=2,即B在反比例解析式y=
上,
则四边形ABCD能成为平行四边形;
(3)证明:∵AC=BD,A(1,4),B(m,n)
∴m=4,又B(m,n)在反比例函数y=
上,
∴B(4,1),
∵AC⊥x轴,BD⊥y轴,
∴E(1,1),即DE=CE=1,
∵AC=BD,
∴AC-EC=BD-DE,即AE=EB=3,
在△DEC和△BAE中,∠CED=∠AEB,
=
=
,
∴△DEC∽△BAE,
∴∠CDE=∠ABE,
∴CD∥AB,
在Rt△ADE和Rt△BCE中,由AE=BE=3,DE=CE=1,
根据勾股定理得:AD=BC=
,
又AD与BC不平行,
则四边形ABCD为等腰梯形.
| k |
| 1 |
∴反比例解析式为y=
| 4 |
| x |
∴BD=m,AE=AC-EC=4-n,
∵S△ABD=
| 1 |
| 2 |
| 1 |
| 2 |
∴2m-
| 1 |
| 2 |
∴n=
| 4 |
| 3 |
则B(3,
| 4 |
| 3 |
(2)四边形ABCD能成为平行四边形.理由为:
若四边形ABCD为平行四边形,则AC、BD互相平分,即E为AC、BD的中点,
∵A(1,4),
∴E(1,2),B(2,2),
将x=2代入反比例解析式得:y=
| 4 |
| 2 |
| 4 |
| x |
则四边形ABCD能成为平行四边形;
(3)证明:∵AC=BD,A(1,4),B(m,n)
∴m=4,又B(m,n)在反比例函数y=
| 4 |
| x |
∴B(4,1),
∵AC⊥x轴,BD⊥y轴,
∴E(1,1),即DE=CE=1,
∵AC=BD,
∴AC-EC=BD-DE,即AE=EB=3,
在△DEC和△BAE中,∠CED=∠AEB,
| DE |
| EB |
| EC |
| AE |
| 1 |
| 3 |
∴△DEC∽△BAE,
∴∠CDE=∠ABE,
∴CD∥AB,
在Rt△ADE和Rt△BCE中,由AE=BE=3,DE=CE=1,
根据勾股定理得:AD=BC=
| 10 |
又AD与BC不平行,
则四边形ABCD为等腰梯形.
点评:此题属于反比例综合题,涉及的知识有:相似三角形的判定与性质,坐标与图形性质,平行四边形的判定与性质,勾股定理,以及等腰梯形的判定,熟练掌握判定与性质是解本题的关键.

练习册系列答案
相关题目
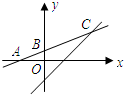 如图,函数y=kx+b的图象与x轴,y轴分别交于A(-2,0),B(0,1)两点,那么此函数的图象与函数y=x-1的图象交点C的坐标是
如图,函数y=kx+b的图象与x轴,y轴分别交于A(-2,0),B(0,1)两点,那么此函数的图象与函数y=x-1的图象交点C的坐标是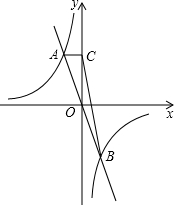 如图,函数y=-kx与
如图,函数y=-kx与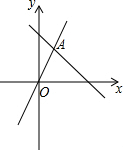 (2013•鄞州区模拟)如图,函数y=kx和y=-
(2013•鄞州区模拟)如图,函数y=kx和y=-