题目内容
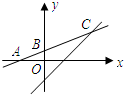 如图,函数y=kx+b的图象与x轴,y轴分别交于A(-2,0),B(0,1)两点,那么此函数的图象与函数y=x-1的图象交点C的坐标是
如图,函数y=kx+b的图象与x轴,y轴分别交于A(-2,0),B(0,1)两点,那么此函数的图象与函数y=x-1的图象交点C的坐标是分析:首先运用待定系数法求得直线y=kx+b的解析式,再进一步和y=x-1联立解方程组求得交点的坐标.
解答:解:∵函数y=kx+b的图象与x轴,y轴分别交于A(-2,0),B(0,1)两点,
∴
,
解,得
.
则直线的解析式是y=
x+1.
根据题意,得
,
解,得
.
则点C的坐标是(4,3).
故答案为:(4,3).
∴
|
解,得
|
则直线的解析式是y=
| 1 |
| 2 |
根据题意,得
|
解,得
|
则点C的坐标是(4,3).
故答案为:(4,3).
点评:此题考查了运用待定系数法求函数解析式的方法以及求两条直线的交点坐标的方法.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
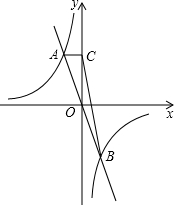 如图,函数y=-kx与
如图,函数y=-kx与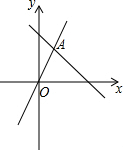 (2013•鄞州区模拟)如图,函数y=kx和y=-
(2013•鄞州区模拟)如图,函数y=kx和y=- 如图,函数y=
如图,函数y=