题目内容
【题目】(1)如图1,在矩形ABCD中,点P为边BC上一点,且![]() ,
, ![]() ,求BP的长;
,求BP的长;
(2)如图2,在平行四边形ABCD中, ![]() ,求
,求![]() 的长;
的长;

(3)如图3,在四边形ABCD中,AD∥BC, ![]() ,
, ![]() ,在BC边上存在一点P,使得
,在BC边上存在一点P,使得![]() ,则边
,则边![]() 的长满足的条件为 。(请直接写出结果)
的长满足的条件为 。(请直接写出结果)

【答案】(1)2;(2)![]() ;(3)
;(3)![]()
【解析】试题分析:(1)由四边形ABCD是矩形,得到∠B=∠C=90°,根据余角的性质得到∠BAP=∠DPC,推出△ABP∽△PCD,根据相似三角形的性质即可得到结论;
(2)延长BC至点E,使得CD⊥DE,通过△ABP∽△DPE,列方程得到BP=1,过点P作PF⊥AB,解直角三角形即可得到结论;
(3)作AE⊥BC,DF⊥BC,得到∠AEP=∠DFP=90°,推出△AEP∽△PFD,根据相似三角形的性质得到AEDF=PEPF=4,由PE+PF≥2 ![]() ,即可得到结论.
,即可得到结论.
试题解析:(1)∵四边形ABCD是矩形,
∴∠B=∠C=90°,
∵∠APD=∠B=90°,
∴∠PAB+∠APB=∠APB+∠DPC=90°,
∴∠BAP=∠DPC,
∴△ABP∽△PCD,
∴![]() ,
,
设BP=x,∴![]()
∴x1=2,x2=8,又BP<PC,
∴BP=2;
(2)延长BC至点E,使得CD⊥DE,
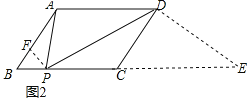
∵AB=2![]() ,BC=5,∠APD=∠B=45°,
,BC=5,∠APD=∠B=45°,
∴∠DPE=∠BAP,∠B=∠E=45°,
∴△ABP∽△DEP,
∴![]() ,
,
设BP=x,CE=![]() CD=4,
CD=4,
∴![]() ,
,
∴BP=1,
过点P作PF⊥AB,
则BF=PF=![]() ,AF=
,AF=![]() ,
,
∴AP=![]() ;
;
(3)AD≥4,
作AE⊥BC,DF⊥BC,
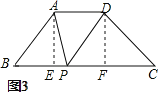
∴∠AEP=∠DFP=90°,
∵∠APD=90°,
∴∠EAP+∠APE=∠APE+∠DPF=90°,
∴∠EAP=∠DPF,
∴△AEP∽△PFD,
∴![]() ,
,
∴AEDF=PEPF=4,
∵PE+PF≥2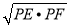 ,
,
∴AD=PE+PF≥4.
故答案为:AD≥4.


