题目内容
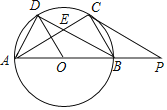
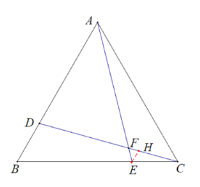
【题目】如图,在等边△ABC中,点D、E分别在边AB、BC上,AD=BE,CD与AE交于F.
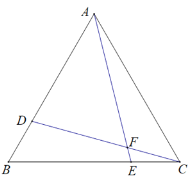
(1)求∠AFD的度数;
(2)若BE=m,CE=n.
①求![]() 的值;(用含有m和n的式子表示)
的值;(用含有m和n的式子表示)
②若![]() =
=![]() ,直接写出
,直接写出![]() 的值.
的值.
【答案】(1)60°;(2)①![]() ;②
;②![]()
【解析】
(1)利用SAS证出△ABE≌△CAD,然后根据全等三角形的性质、四边形的内角和和等边三角形的性质即可求出结论;
(2)过点E作EH∥AB交CD于点H,可证△CEH∽△CBD,△FEH∽△FAD,然后列出比例式,结合(1)中全等即可求出结论;
(3)根据(2)的结论可设![]() ,然后根据相似三角形的判定定理证出△AFD∽ABE,列出比例式即可求出a的值,然后用m和n表示出EF和DF,再结合已知条件即可求出结论.
,然后根据相似三角形的判定定理证出△AFD∽ABE,列出比例式即可求出a的值,然后用m和n表示出EF和DF,再结合已知条件即可求出结论.
解(1)∵△ABC为等边三角形,
∴AB=BC=AC,∠B=∠BCA=∠BAC=60°
又AD=BE,
∴△ABE≌△CAD,
∴∠ADC=∠BEA
∵∠BDF+∠ADC =180°
∴∠BDF+∠BEF=180°,
∴∠B+∠DFE=180°,
∵∠AFD+∠DFE=180°,
∴∠AFD=∠B=60°
(2)过点E作EH∥AB交CD于点H,
∴△CEH∽△CBD,△FEH∽△FAD,
∴![]() ,
,![]()
由(1)△ABE≌△CAD,
∴AD=BE=m,则BD=CE=n,
∴![]() ,
,![]() ,
,
∴![]()
(3)∵![]()
可设![]()
则AE=AF+EF=![]()
∵∠AFD=∠B=60°,∠DAF=∠EAB
∴△AFD∽ABE
∴![]()
即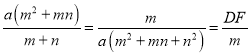
解得:![]()
∴![]() ,
,
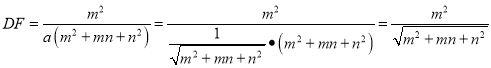
∵![]() =
=![]()
∴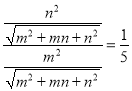
整理,得![]()
∴![]() 或
或![]() (不符合实际,舍去)
(不符合实际,舍去)

练习册系列答案
相关题目