��Ŀ����
����Ŀ��ij���ܻ��س����������Ի��ܣ�̫�����ļ۸�Ϊ6Ԫ/�������ļ۸�Ϊ10Ԫ/������һ���Թ���������20��ʱ������20��IJ�������8����
(1)�ֱ�д�����ֻ��ܵĸ�����y(Ԫ)���ڹ�����x(��)�ĺ�������ʽ��
(2)Ϊ��������������С���ƻ����û��ع��������ֻ��ܹ�90��������̫��������������������������һ���������ֻ��ܸ��������ʱ���ܷ������٣������ܷ���Ϊ����Ԫ��
���𰸡���1��y=6x��y=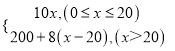 ��2����x��60������������60��������̫����30��ʱ���ܷ��������������ܷ���Ϊ700Ԫ
��2����x��60������������60��������̫����30��ʱ���ܷ��������������ܷ���Ϊ700Ԫ
�����������������(1)��̫�����ļ۸�=6�����������ļ۸��x��20��x��20��������ֱ���м��㣬�ó���������ʽ��(2)��������̫������������m�裬������������(90-m)�裬�������ֻ����ܷ�����wԪ�������������m��ȡֵ��Χ��Ȼ��ó�w��m�ĺ�����ϵʽ��Ȼ�����һ�κ����������Եó���Сֵ.
���������(1)��y̫����=6x��
��y����=10x��x��20����
��y����=10��20+10��0.8����x-20��=200+8x-160=8x+40��x��20��
(2)���������⣬ ��̫������������m�裬������������(90-m)�裬�������ֻ����ܷ�����wԪ��
��m��![]() (90-m) ��m��30��
(90-m) ��m��30��
��w=6m+[8��90-m��+40]=760-2m
��-2��0 ��w����m���������С�� ����m=30ʱ��
w��С=760-2��30=700��Ԫ����
��̫����30�裬����60��ʱ���ܷ������٣����ٷ�����700Ԫ��

 �¿α�������������ҵ�������γ�����ϵ�д�
�¿α�������������ҵ�������γ�����ϵ�д� ����ν����Ž̲��㽭���̴�ѧ������ϵ�д�
����ν����Ž̲��㽭���̴�ѧ������ϵ�д� �����Ļ������������������ϵ�д�
�����Ļ������������������ϵ�д�