题目内容
【题目】在△ABC中,AB=4,AC=3,BC=5,动点P从点C出发,沿着CB方向运动,速度为每秒3个单位,到达点B时运动停止,设运动时间为t秒,请解答下列问题:
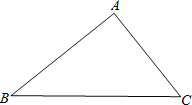
(1)求BC上的高;
(2)当t为何值时,△ACP为等腰三角形?
【答案】(1)2.4;(2)t=1,![]() ,
,![]() .
.
【解析】
试题分析:(1)直接利用勾股定的逆定理得出△ABC是直角三角形,进而利用三角形面积得出答案;
(2)分别利用①当AP=AC时,②当AC=CP′时,③当AP″=CP″时,结合锐角三角函数关系得出答案.
解:(1)∵32+42=52,
∴△ABC是直角三角形,
设BC上的高为x,则![]() ×AB×AC=
×AB×AC=![]() ×BC×x,
×BC×x,
![]() =
=![]() x,
x,
解得:x=2.4,
故BC边上高为2.4;
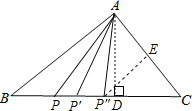
(2)①当AP=AC时,过A作AD⊥BC,
∵cosC=![]() =
=![]() ,
,
∴CD=ACcosC=3×![]() =
=![]() ,
,
∴CP=![]() ,
,
∵P的速度为每秒3个单位,
∴t=![]() ÷3=
÷3=![]() ;
;
②当AC=CP′时,
∵AC=3,
∴CP′=3,
∴t=3÷3=1;
③当AP″=CP″时,
过P″作P″E⊥AC,
∵AC=3,AP″=CP″,
∴EC=1.5,
∵cosC=![]() =
=![]()
CP″=![]() =
=![]() =2.5,
=2.5,
则t=2.5÷3=![]()
综上所述:t=1,![]() ,
,![]() .
.

练习册系列答案
相关题目