��Ŀ����
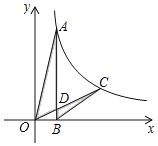
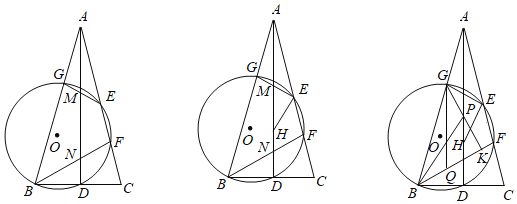
����Ŀ����ͼ����ABC�У�AB��AC��AD��BC��D��E��AC����һ�㣬��O��B��D��E���㣬�ֱ�AC��AB�ڵ�F��G������EG��BF�ֱ���AD���ڵ�M��N��
��1����֤����AMG����BND��
��2������EΪAC���е㣬��֤��BF��BC��
��3���ڣ�2���������£���EH��EG��AD�ڵ�H����EH��EG��4![]() ������G��GK��BF�ڵ�K����P���߶�GK�ϣ���Q���߶�BK�ϣ�����BP��GQ������KGQ��2��GBP��GQ��15
������G��GK��BF�ڵ�K����P���߶�GK�ϣ���Q���߶�BK�ϣ�����BP��GQ������KGQ��2��GBP��GQ��15![]() ����GP�ij��ȣ�
����GP�ij��ȣ�
���𰸡���1������������2������������3��![]()
��������
��1������Բ�ڽ��ı��ε����ʺͲ��ǵ����ʿ�֤��BFE����AGE���ٸ����������ڽǺͶ�����֤��AMG����ANF�������ɵý��ۣ�
��2������DE����֤��BD��CD���ɵ���FBC����BAC��֤����BFC����ABC����C�����۵�֤��
��3��ȡAB�е�P������MH��GH��DE���ɵ�ƽ���ı���BDEM���ȱ���MHE���ɵó���GAH����GHA��15�������GA��GH��![]() EH��
EH��![]() �����AE��
�����AE��![]() �������AB��BG����Rt��BGK�У��ɵ���GBK��45�������GK��BK��
�������AB��BG����Rt��BGK�У��ɵ���GBK��45�������GK��BK��![]() ��Rt��QGK�й��ɶ����ɵ�QK��
��Rt��QGK�й��ɶ����ɵ�QK��![]() ���ӳ�BK��TʹKT��PK������GK����BKP�ա�GKT���ó���KGT����KBP���ɵ�QG��QT��15
���ӳ�BK��TʹKT��PK������GK����BKP�ա�GKT���ó���KGT����KBP���ɵ�QG��QT��15![]() ����PK�������GP��GK��PK��
����PK�������GP��GK��PK��![]() ��
��
��1��֤������AB��AC��AD��BC��
���BAD����CAD��
���ı���BFEG�ڽ�����O��
���BGE+��BFE��180��
�ߡ�BGE+��AGE��180����
���BFE����AGE��
�ߡ�AGM�У���BAD+��AGE+��AMG��180����
��ANF����CAD+��BFE+��ANF��180����
���AMG����ANF��
�ߡ�ANF����BND��
���AMG����BND��
��2��֤������ͼ������DE��
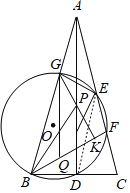
��AB��AC��AD��BC��
��BD��CD��
��AE��CE��
��DE����ABC����λ�ߣ�
��DE��AB��
���DEC����BAC��
�ߡ�DEC����FBC��
���FBC����BAC��
�ߡ�C=��C��
���ABC�ס�BFC��
���ABC=��BFC��
��AB��AC��
���ABC����C��
���BFC����ABC����C��
��BF��BC��
��3���⣺��ͼ��ȡAB�е�M������MH��ME��DE��
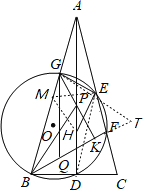
��AE��CE��AM=BM��
��ME�ǡ�ABC����λ�ߣ�
��ME��BD��
���GME����ABC��
�ߡ�ABC����C����C����EDC����BGE��
���MGE����GME��
��GE��ME��
��MH��ME��EH��EG��
���MHE�ǵȱ������Σ�
��AD��ֱƽ��BC��
��AH��ֱƽ��ME��
���GAH����GHA��15����
![]() EH��
EH��![]() ��
��![]() ��
��
������AGE��AE��![]() ��
��
��AB��AC��![]() ��
��
��BG��AB��AG��![]() ��
��
��Rt��BGK�У��ɵ���GBK��45����
��GK��BK��![]() ��
��
��Rt��QGK��QK��![]() ��
��![]() ��
��
�ӳ�BK��TʹKT��PK������GK��
�ߡ�BKP����GKT��
���BKP�ա�GKT��SAS����
���KGT����KBP�����BPK����GTK��
�ߡ�QGT����KGQ+��KGT����KGQ+��PBK��
��KGQ��2��GBP��
���QGT��2��GBP+��PBK��
�ߡ�PBK��45������GBP��
���QGT��45��+��PBG����BPK��
���QGT����GTK��
��QG��QT��15![]() ��
��
��PK��KT��QT��QK��![]() ��
��
��GP��GK��PK��12![]() ��
��![]() ��
��