题目内容
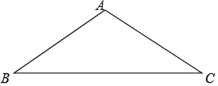
【题目】在正方形 ABCD 中,M 是 BC 边上一点,且点 M 不与 B、C 重合,点 P 在射线 AM 上,将线段 AP 绕点 A 顺时针旋转 90°得到线段 AQ,连接BP,DQ.
(1)依题意补全图 1;
(2)①连接 DP,若点 P,Q,D 恰好在同一条直线上,求证:DP2+DQ2=2AB2;
②若点 P,Q,C 恰好在同一条直线上,则 BP 与 AB 的数量关系为: .
【答案】(1)详见解析;(2)①详见解析;②BP=AB.
【解析】
(1)根据要求画出图形即可;
(2)①连接BD,如图2,只要证明△ADQ≌△ABP,∠DPB=90°即可解决问题;
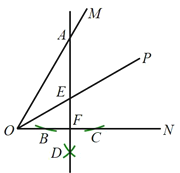
②结论:BP=AB,如图3中,连接AC,延长CD到N,使得DN=CD,连接AN,QN.由△ADQ≌△ABP,△ANQ≌△ACP,推出DQ=PB,∠AQN=∠APC=45°,由∠AQP=45°,推出∠NQC=90°,由CD=DN,可得DQ=CD=DN=AB;
(1)解:补全图形如图 1:
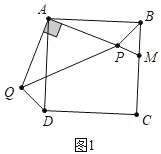
(2)①证明:连接 BD,如图 2,
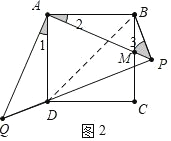
∵线段 AP 绕点 A 顺时针旋转 90°得到线段 AQ,
∴AQ=AP,∠QAP=90°,
∵四边形 ABCD 是正方形,
∴AD=AB,∠DAB=90°,
∴∠1=∠2.
∴△ADQ≌△ABP,
∴DQ=BP,∠Q=∠3,
∵在 Rt△QAP 中,∠Q+∠QPA=90°,
∴∠BPD=∠3+∠QPA=90°,
∵在 Rt△BPD 中,DP2+BP2=BD2, 又∵DQ=BP,BD2=2AB2,
∴DP2+DQ2=2AB2.
②解:结论:BP=AB.
理由:如图 3 中,连接 AC,延长 CD 到 N,使得 DN=CD,连接 AN,QN.
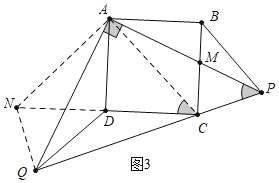
∵△ADQ≌△ABP,△ANQ≌△ACP,
∴DQ=PB,∠AQN=∠APC=45°,
∵∠AQP=45°,
∴∠NQC=90°,
∵CD=DN,
∴DQ=CD=DN=AB,
∴PB=AB.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】近年来网约车十分流行,初三某班学生对“美团”和“滴滴”两家网约车公司各10名司机月收入进行了一项抽样调查,司机月收入(单位:千元)如图所示:

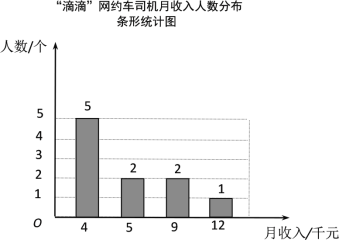
根据以上信息,整理分析数据如下:
平均月收入/千元 | 中位数/千元 | 众数/千元 | 方差/千元2 | |
“美团” | ① | 6 | 6 | 1.2 |
“滴滴” | 6 | ② | 4 | ③ |
(1)完成表格填空;
(2)若从两家公司中选择一家做网约车司机,你会选哪家公司,并说明理由.