题目内容
【题目】如图,B为线段AD上一点,△ABC和△BDE都是等边三角形,连接CE并延长,交AD的延长线于F,△ABC的外接圆⊙O交CF于点M.

(1)求证:BE是⊙O的切线;
(2)求证:AC2=CMCF.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
试题分析:(1)连接OB,只要证明∠OBE=90°即可求解;
(2)连接MB,易证∠CMB=∠CBF,则可以得到△CMB∽△CBF,根据相似三角形对应边的比相等即可得证.
试题解析:(1)连结OB,
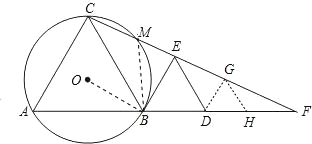
∵△ABC和△BDE都是等边三角形,
∴∠ABC=∠EBD=60°,
∴∠CBE=60°,∠OBC=30°,
∴∠OBE=90°,
∴BE是⊙O的切线;
(2)连结MB,则∠CMB=180°-∠A=120°
∵∠CBF=60°+60°=120°
∴∠CMB=∠CBF
∵∠BCM=∠FCB
∴△CMB∽△CBF
∴![]() ,即CB2=CMCF,
,即CB2=CMCF,
∵AC=CB
∴AC2=CMCF.

练习册系列答案
相关题目
【题目】某射击队要从甲,乙,丙,丁四名队员中选出一名队员代表射击队参加射击比赛,各队员的平时成绩的平均数及方差如表所示:
甲 | 乙 | 丙 | 丁 | |
平均数(环) | 9.8 | 9.3 | 9.6 | 9.8 |
方差(环2) | 3.3 | 3.3 | 3.5 | 6.1 |
根据表中数据,要从这四个队员中选择一个成绩好且发挥稳定的队员去参赛,那么应该选的队员是( )
A. 甲B. 乙C. 丙D. 丁
