题目内容
（1）图1是由若干个小圆圈堆成的一个形如等边三角形的图案，最上面一层有一个圆圈，以下各层均比上一层多一个圆圈，一共堆了n层．将图1倒置后与原图1拼成图2的形状，这样我们可以算出图1中所有圆圈的个数为：1+2+3+…+n=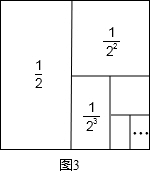
（2）运用第（1）题的结论，试求1+2+3+…+99的值；
（3）在一次数学活动中，为了求
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 24 |
| 1 |
| 25 |
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 24 |
| 1 |
| 25 |
| 1 |
| 2n |
（4）运用第（3）题的结论，试求
| 5 |
| 6 |
| 11 |
| 12 |
| 23 |
| 24 |
| 47 |
| 48 |
| 95 |
| 96 |
| 191 |
| 192 |
分析：（1）看图2可得圆圈共有n层，每层有（n+1）个，求得n层圆圈的个数，除以2即可；
（2）利用（1）得到的公式计算即可；
（3）让最大的正方形的面积减去最小的长方形的面积即可；
（4）先整理为分子为1的形式，进而整理为分母为底数为2的幂的形式，利用（3）的结论作答即可．
（2）利用（1）得到的公式计算即可；
（3）让最大的正方形的面积减去最小的长方形的面积即可；
（4）先整理为分子为1的形式，进而整理为分母为底数为2的幂的形式，利用（3）的结论作答即可．
解答：解：（1）平行四边形中圆圈的个数为n（n+1），
∴图1中所有圆圈的个数为：1+2+3+…+n=
，
故答案为
；
（2）1+2+3+…+99=
=4950；
（3）
+
+
+
+
+…+
=1-
，
故答案为1-
；
（4）
+
+
+
+
+
=1-
+1-
+1-
+1-
+1-
+1-
=6-
（
+
+…+
）=6-
×（1-
）=
．
∴图1中所有圆圈的个数为：1+2+3+…+n=
| n(n+1) |
| 2 |
故答案为
| n(n+1) |
| 2 |
（2）1+2+3+…+99=
| 99×100 |
| 2 |
（3）
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 24 |
| 1 |
| 25 |
| 1 |
| 2n |
| 1 |
| 2n |
故答案为1-
| 1 |
| 2n |
（4）
| 5 |
| 6 |
| 11 |
| 12 |
| 23 |
| 24 |
| 47 |
| 48 |
| 95 |
| 96 |
| 191 |
| 192 |
| 1 |
| 6 |
| 1 |
| 12 |
| 1 |
| 24 |
| 1 |
| 48 |
| 1 |
| 96 |
| 1 |
| 192 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 26 |
| 1 |
| 3 |
| 1 |
| 26 |
| 363 |
| 64 |
点评：考查有关规律性的计算；根据所给图形得到计算的规律是解决本题的关键．
练习册系列答案
相关题目
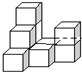18、如图，是由若干个完全相同的小正方体组成的一个几何体．
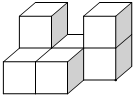如图，是由若干个大小相同且边长为1的小正方体堆砌而成的几何体，那么其三种视图的面积之和是（ ）
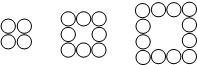2008年奥运期间，小区物业用花盆妆点院落．下列的每一个图都是由若干个花盆组成的正方形图案．