题目内容
20、下列各图都是由若干个木条钉成的多边形木框,要想把它们固定住,那么至少要用多少条木条才能保持木框的稳定性,设多边形的边数为n,所用的木条数为m,请填空:

当n=3时,m=
写出多边形木框的木条数n与m的关系式为

当n=3时,m=
0
;当n=4时,m=1
;当n=5时,m=2
;写出多边形木框的木条数n与m的关系式为
m=n-3
.分析:根据三角形具有稳定性,其它多边形不具有稳定性,把多边形分割成三角形,则多边形的形状就不会改变作出判断.
解答:解:如图所示:
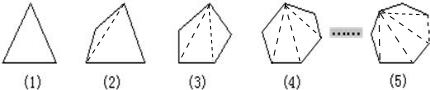
当n=3时,m=0;当n=4时,m=1;当n=5时,m=2;
…
则多边形木框的木条数n与m的关系式为m=n-3.
故答案为:0;1;2;m=n-3.

当n=3时,m=0;当n=4时,m=1;当n=5时,m=2;
…
则多边形木框的木条数n与m的关系式为m=n-3.
故答案为:0;1;2;m=n-3.
点评:本题考查规律型:图形的变化,解题的关键是结合三角形稳定性的特点,要使一些图形具有稳定的结构,往往通过连接辅助线转化为三角形而获得.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
图1是由若干个小圆圈堆成的一个图案,最上面一层有2个圆圈,以下各层均比上一层多一个圆圈,一共堆了n层.完成下列问题:
(1)每一层的圆圈个数与层数的关系为:
| 层数 | 1 | 2 | 3 | … | n |
| 每层圆圈个数 | … |
将图1倒置后与原图1拼成图2的形状,则图2中每层圆圈个数为________;n层圆圈总数为________;由于图2中圆圈个数是图1中的________倍,可以得出图1中所有圆圈的个数为________.
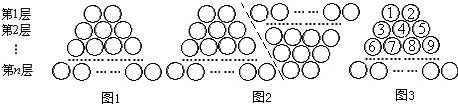
(3)假设图1中的圆圈共有10层,我们自上往下,在每个圆圈中都按图3的方式填上一串连续的正整数1,2,3,4,…,则最底层从左边数第三个圆圈中的数是________.


