题目内容
【题目】定义:把函数y=bx+a和函数y=ax+b(其中a,b是常数,且a≠0,b≠0)称为一对交换函数,其中一个函数是另一个函数的交换函数.比如,函数y=4x+1是函数y=x+4的交换函数,等等.
(1)直接写出函数y=2x+1的交换函数;_________________;并直接写出这对交换函数和x轴所围图形的面积为_____________________________;
(2)若一次函数y=ax+2a和其交换函数与x轴所围图形的面积为3,求a的值.
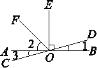
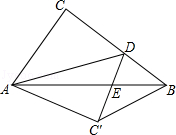
(3)如图,在平面直角坐标xOy中,矩形OABC中,点C(0, ![]() ),M、N分别是线段OC、AB的中点,将△ABD沿着折痕AD翻折,使点B的落点E恰好落在线段MN的中点,点F是线段BC的中点,连接EF,若一次函数
),M、N分别是线段OC、AB的中点,将△ABD沿着折痕AD翻折,使点B的落点E恰好落在线段MN的中点,点F是线段BC的中点,连接EF,若一次函数![]() 和
和![]() 与线段EF始终都有交点,则m的取值范围为_____________________.
与线段EF始终都有交点,则m的取值范围为_____________________.
【答案】 ![]() ,
, ![]()
![]()
![]()
【解析】(1)根据交换函数的定义即可求解;(2)根据![]() 和其交换函数与
和其交换函数与![]() 轴所围图形的面积为3,结合三角形的面积公式的求法即可得出答案.(3)由折叠的性质可得AB=AE,再由直线
轴所围图形的面积为3,结合三角形的面积公式的求法即可得出答案.(3)由折叠的性质可得AB=AE,再由直线![]() 为矩形
为矩形![]() 的对称轴可得
的对称轴可得![]() 为等边三角形,然后利用勾股定理求出点E,F的坐标,结合一次函数和与线段EF的交点即可求出m的取值范围.
为等边三角形,然后利用勾股定理求出点E,F的坐标,结合一次函数和与线段EF的交点即可求出m的取值范围.
解:(![]() )
)![]() ;
; ![]() ;
;
(![]() )
)![]() 其交换函数为
其交换函数为![]() ,
,
与![]() 轴交点分别为
轴交点分别为![]() ,
, ![]() ,
,
![]()
解之得![]() ,
,
∴![]() ,
,
![]() .
.
(![]() )连接
)连接![]() ,
,
由翻折可得![]() .
.
∵![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 中点,
中点,
∴直线![]() 为矩形
为矩形![]() 的对称轴,
的对称轴,
∴![]() ,
,
∴![]() 为等边三角形,
为等边三角形,
∴![]() ,
,
∴![]() .
.
在![]() 中,
中, ![]() ,
,
![]() ,
,
∴ ,
,  .
.
∵![]() 和
和![]() 与
与![]() 线段始终有交点,
线段始终有交点,
当![]() 时,
时, ![]() ,
,
∴![]() ,
,
![]() .
.

 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案【题目】阅读下列材料:
近五年,我国对外贸易发展迅速.据海关统计,2017年我国进出口总额为27.8万亿元,比2016年增长14.4%,其中2017年进口额12.5万亿元,比2016年增长19.0%.2013---2016年我国进出口额数据如下表:
年份 | 2013 | 2014 | 2015 | 2016 |
出口额/万亿元 | 13.7 | 14.4 | 14.1 | 13.8 |
进口额/万亿元 | 12.1 | 12.0 | 10.4 | 10.5 |
根据以上材料解答下列问题:
(1)2017年我国出口额为______________万亿元;
(2)请选择适当的统计图描述2013---2017年我国出口额,并在图中标明相应数据;
(3)通过(2)中的统计图判断:2013---2017年我国出口额比上一年增长最多的是_______________年.