题目内容
【题目】如图，直线AB，CD相交于点O，OE⊥AB，垂足为O，OF平分∠AOE，∠1＝15°，则下列结论中不正确的是( )
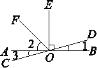
A. ∠2＝45° B. ∠1＝∠3 C. ∠EOD与∠3互为余角 D. ∠FOD＝110°
【答案】D
【解析】根据垂直的定义可得∠AOE=90°，再根据角平分线的定义求出∠2=45°，根据对顶角相等可得∠1=∠3，根据互余的定义求出∠EOD与∠3互为余角，根据平角等于180°列式计算即可求出∠FOD=120°．
A、∵OE⊥AB，
∴∠AOE=90°，
∵OF平分∠AOE，
∴∠2=
∠AOE=×90°=45°，故本选项错误；
B、∵∠1、∠3是对顶角，
∴∠1=∠3，故本选项错误；
C、∵∠EOD+∠1=∠BOE=90°，
∴∠EOD+∠3=90°，
∴∠EOD与∠3互为余角，故本选项错误；
D、∠FOD=180°-∠1-∠2=180°-15°-45°=120°，故本选项正确．
故选：D．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
【题目】下表记录了一名球员在罚球线上投篮的结果，
投篮次数（n） | 50 | 100 | 150 | 209 | 250 | 300 | 350 |
投中次数（m） | 28 | 60 | 78 | 104 | 123 | 152 | 175 |
投中频率（n/m） | 0.56 | 0.60 |
| 0.49 |
|
|
（1）计算并填写表中的投中频率（精确到0.01）；
（2）这名球员投篮一次，投中的概率约是多少（精确到0.1）？
