题目内容
【题目】如图,在长方形ABCD中,AB=6,CB=8,点P与点Q分别是AB、CB边上的动点,点P与点Q同时出发,点P以每秒2个单位长度的速度从点A→点B运动,点Q以每秒1个单位长度的速度从点C→点B运动.当其中一个点到达终点时,另一个点随之停止运动.(设运动时间为t秒) 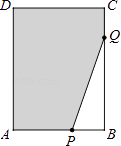
(1)如果存在某一时刻恰好使QB=2PB,求出此时t的值;
(2)在(1)的条件下,求图中阴影部分的面积(结果保留整数).
【答案】
(1)解:由题意可知AP=2t,CQ=t,
∴PB=AB﹣AP=6﹣2t,QB=CB﹣CQ=8﹣t.
当QB=2PB时,有8﹣t=2(6﹣2t).
解这个方程,得 ![]() .
.
所以当 ![]() 秒时,QB=2PB
秒时,QB=2PB
(2)解:当 ![]() 时,
时, ![]() ,
,
![]() .
.
∴ ![]() .
.
∵S长方形ABCD=ABCB=6×8=48,
∴S阴影=S长方形ABCD﹣S△QPB≈37
【解析】(1)当t秒QB=2PB时,BP=6﹣2t,BQ=8﹣t,就有8﹣t=2(6﹣2t),求出结论就可以了;(2)由(1)求出t的值就可以求出BP、BQ的值,根据矩形的面积减去三角形BPQ的面积就可以求出结论.
【考点精析】利用两点间的距离和三角形的面积对题目进行判断即可得到答案,需要熟知同轴两点求距离,大减小数就为之.与轴等距两个点,间距求法亦如此.平面任意两个点,横纵标差先求值.差方相加开平方,距离公式要牢记;三角形的面积=1/2×底×高.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案
相关题目