题目内容
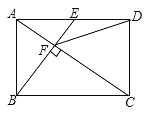
【题目】如图,在矩形![]() 中,
中,![]() 是
是![]() 边的中点,
边的中点,![]() 于点
于点![]() ,连接
,连接![]() .下列结论不正确的是( )
.下列结论不正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
由于AE∥BC,则根据相似三角形的判定可对A选项进行判断;利用相似三角形的性质可对B选项进行判断;作DH⊥AC于H,如图,证明EF∥DH,则根据平行线分线段成比例定理得到AF=FH,则可证明DH垂直平分CF,从而可对C选项进行判断;设AF=x,则FH=CH=x,利用摄影定理可计算出DH=![]() ,然后根据正切的定义可对D进行判断.
,然后根据正切的定义可对D进行判断.
∵四边形ABCD为矩形,
∴AD∥BC,AD=BC,∠ABC=90°
∵E是AD边的中点,
∴BC=AD=2AE,
∵AE∥BC,
∴∠ACB=∠FAE
∵![]()
∴∠AFE=90°
∴∠AFE=∠ABC=90°
∴△AEF∽△CAB,所以A选项的结论正确;
∴![]() ,
,
∴CF=2AF,所以B选项的结论正确;
作DH⊥AC于H,如图,
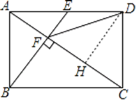
∵BE⊥AC,
∴EF∥DH,
![]() ,
,
即AF=FH,
而CF=2AF,
∴CH=FH,
∴DH垂直平分CF,
∴DF=DC,所以C选项的结论正确;
∵四边形ABCD是矩形,
∴∠ADC=90°,
∴∠ADH+∠CDH=90°,
∵DH⊥AC,
∴∠AHD=∠CHD=90°
∴∠HAD+∠HAD=90°,
∴∠HAD=∠CDH,
∴△AHD∽△DHC
∴![]()
设AF=x,则FH=CH=x,
∴DH2=AHCH=2xx,
∴DH=![]()
在Rt△AHD中,![]() ,
,
即![]() ,所以D选项的结论错误.
,所以D选项的结论错误.
故选:D.

练习册系列答案
相关题目