题目内容
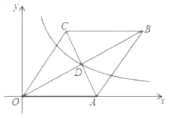
【题目】如图,直线![]() 与
与![]() 轴所夹的锐角为
轴所夹的锐角为![]() 的长为
的长为![]()
![]() ,均为等边三角形,点
,均为等边三角形,点![]() 在
在![]() 轴的正半轴上一次排列,点
轴的正半轴上一次排列,点![]() 在直线
在直线![]() 上依次排列,那么点
上依次排列,那么点![]() 的坐标为__________.
的坐标为__________.
【答案】![]()
【解析】
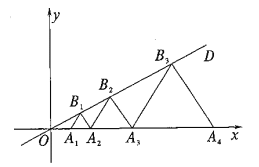
根据等边三角形的性质和∠B1OA2=30°,可求得∠B1OA2=∠A1B1O=30°,可求得OA2=2OA1=2,同理可求得OAn=2n-1,再结合含30°角的直角三角形的性质可求得△AnBnAn+1的边长,进一步可求得点Bn的坐标.
∵△A1B1A2为等边三角形,
∴∠B1A1A2=60°,
∵∠B1OA2=30°,
∴∠B1OA2=∠A1B1O=30°,可求得OA2=2OA1=2,
同理可求得OAn=2n-1,
∵∠BnOAn+1=30°,∠BnAnAn+1=60°,
∴∠BnOAn+1=∠OBnAn=30°
∴BnAn=OAn=2n-1,
即△AnBnAn+1的边长为2n-1,则可求得其高为![]() ,
,
∴点Bn的横坐标为![]() ,
,
∴点Bn的坐标为![]() .
.
故答案为![]() .
.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目