Question

【题目】如图1，已知直线y=x+3与x轴交于点A，与y轴交于点B，抛物线y=﹣x2+bx+c经过A、B两点，与x轴交于另一个点C，对称轴与直线AB交于点E，抛物线顶点为D．

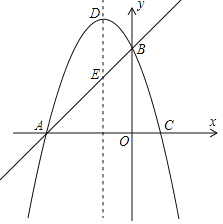
（1）求抛物线的解析式；

（2）在第三象限内，F为抛物线上一点，以A、E、F为顶点的三角形面积为3，求点F的坐标；

（3）点P从点D出发，沿对称轴向下以每秒1个单位长度的速度匀速运动，设运动的时间为t秒，当t为何值时，以P、B、C为顶点的三角形是直角三角形？直接写出所有符合条件的t值．

Answer 1

【答案】（1）y=﹣x2﹣2x+3

（2）点F的坐标为（，）

（3）当t为秒或2秒或3秒或秒时，以P、B、C为顶点的三角形是直角三角形。

【解析】

试题（1）先由直线AB的解析式为y=x+3，求出它与x轴的交点A、与y轴的交点B的坐标，再将A、B两点的坐标代入y=﹣x2+bx+c，运用待定系数法即可求出抛物线的解析式。

∵y=x+3与x轴交于点A，与y轴交于点B，

∴当y=0时，x=﹣3，即A点坐标为（﹣3，0），当x=0时，y=3，即B点坐标为（0，3）。

将A（﹣3，0），B（0，3）代入y=﹣x2+bx+c，得

，解得。

∴抛物线的解析式为y=﹣x2﹣2x+3。

（2）设第三象限内的点F的坐标为（m，﹣m2﹣2m+3），运用配方法求出抛物线的对称轴及顶点D的坐标，再设抛物线的对称轴与x轴交于点G，连接FG，根据S△AEF=S△AEG+S△AFG﹣S△EFG=3，列出关于m的方程，解方程求出m的值，进而得出点F的坐标。

如图1，设第三象限内的点F的坐标为（m，﹣m2﹣2m+3），

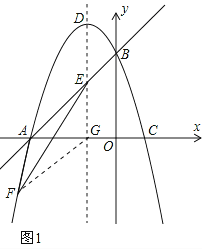
则m＜0，﹣m2﹣2m+3＜0。

∵y=﹣x2﹣2x+3=﹣（x+1）2+4，

∴对称轴为直线x=﹣1，顶点D的坐标为（﹣1，4）。

设抛物线的对称轴与x轴交于点G，连接FG，

则G（﹣1，0），AG=2。

∵直线AB的解析式为y=x+3，

∴当x=﹣1时，y=﹣1+3=2。∴E点坐标为（﹣1，2）。

∵S△AEF=S△AEG+S△AFG﹣S△EFG

=×2×2+×2×（m2+2m﹣3）﹣×2×（﹣1﹣m）=m2+3m，

∴以A、E、F为顶点的三角形面积为3时，m2+3m=3，

解得m1=，m2=（舍去）。

当m=时，﹣m2﹣2m+3=﹣m2﹣3m+m+3=﹣3+m+3=m=。

∴点F的坐标为（，）。

（3）设P点坐标为（﹣1，n），．

∵B（0，3），C（1，0），∴BC2=12+32=10。

分三种情况：

①如图2，如果∠PBC=90°，那么PB2+BC2=PC2，

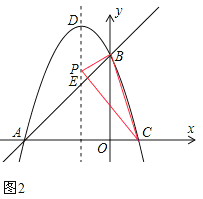
即（0+1）2+（n﹣3）2+10=（1+1）2+（n﹣0）2，

化简整理得6n=16，解得n=。

∴P点坐标为（﹣1，）。

∵顶点D的坐标为（﹣1，4），

∴PD=4﹣=。

∵点P的速度为每秒1个单位长度，∴t1=秒。

②如图3，如果∠BPC=90°，那么PB2+PC2=BC2，

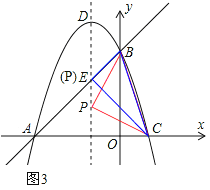
即（0+1）2+（n﹣3）2+（1+1）2+（n﹣0）2=10，

化简整理得n2﹣3n+2=0，解得n=2或1。

∴P点坐标为（﹣1，2）或（﹣1，1），

∵顶点D的坐标为（﹣1，4），

∴PD=4﹣2=2或PD=4﹣1=3。

∵点P的速度为每秒1个单位长度，∴t2=2秒，t3=3秒。

③如图4，如果∠BCP=90°，那么BC2+PC2=PB2，

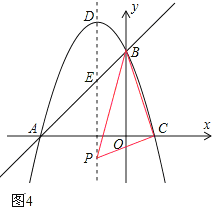
即10+（1+1）2+（n﹣0）2=（0+1）2+（n﹣3）2，

化简整理得6n=﹣4，解得n=。

∴P点坐标为（﹣1，）。

∵顶点D的坐标为（﹣1，4），∴PD=4+=。

∵点P的速度为每秒1个单位长度，

∴t4=秒。

综上所述，当t为秒或2秒或3秒或秒时，以P、B、C为顶点的三角形是直角三角形。