题目内容
【题目】如图,已知在矩形ABCD中,AB=2,BC=3,P是线段AD上的一动点,连接PC,过点P作PE⊥PC交AB于点E.以CE为直径作⊙O,当点P从点A移动到点D时,对应点O也随之运动,则点O运动的路程长度为_____.

【答案】![]() .
.
【解析】
连接AC,取AC的中点K,连接OK.设AP=x,AE=y,求出AE的最大值,求出OK的最大值,由题意点O的运动路径的长为2OK,由此即可解决问题.
解:连接AC,取AC的中点K,连接OK.设AP=x,AE=y,
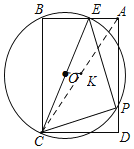
∵PE⊥CP
∴∠APE+∠CPD=90°,且∠AEP+∠APE=90°
∴∠AEP=∠CPD,且∠EAP=∠CDP=90°
∵△APE∽△DCP
∴![]() ,
,
即x(3﹣x)=2y,
∴y=![]() x(3﹣x)=﹣
x(3﹣x)=﹣![]() x2+
x2+![]() x=﹣GXdjs4436236(x﹣
x=﹣GXdjs4436236(x﹣![]() )2+
)2+![]() ,
,
∴当x=![]() 时,y的最大值为
时,y的最大值为![]() ,
,
∴AE的最大值=![]() ,
,
∵AK=KC,EO=OC,
∴OK=![]() AE=
AE=![]() ,
,
∴OK的最大值为![]() ,
,
由题意点O的运动路径的长为2OK=![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目