题目内容
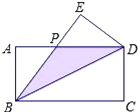
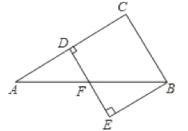
【题目】如图.△ABC中,AC的垂直平分线分别交AC、AB于点D. F,BE⊥DF交DF的延长线于点E,已知∠A=30°，BC=2，AF=BF，则四边形BCDE的面积是_____
【答案】2
【解析】
由AF=BF得到F为AB的中点，又DF垂直平分AC，得到D为AC的中点，可得出DF为三角形ABC的中位线，根据三角形中位线定理得到DF平行于CB，且DF等于BC的一半，由BC的长求出DF的长，由两直线平行同旁内角互补得到∠C=90°，同时由DE与EB垂直，ED与DC垂直，根据垂直的定义得到两个角都为直角，利用三个角为直角的四边形为矩形得到四边形BCDE为矩形，在直角三角形ADF中，利用锐角三角函数定义及特殊角的三角函数值，由∠A=30°，DF的长，求出AD的长，即为DC的长，由矩形的长BC于宽CD的乘积即可求出矩形BCED的面积．
∵AF=BF，即F为AB的中点，又DE垂直平分AC，即D为AC的中点，
∴DF为三角形ABC的中位线，
∴DE∥BC,DF=
BC，
又∠ADF=90°，
∴∠C=∠ADF=90°，
又BE⊥DE，DE⊥AC，
∴∠CDE=∠E=90°，
∴四边形BCDE为矩形，
∵BC=2,∴DF= BC=1，
在Rt△ADF中,∠A=30°，DF=1，
∴tan30°=
,即AD= ，
∴CD=AD=，
则矩形BCDE的面积S=CDBC=2.
故答案为：2
超能学典应用题题卡系列答案
【题目】某学校欲招聘一名新教师，对甲、乙、丙三名应试者进行了面试、笔试和才艺三个方面的量化考核，他们的各项得分（百分制）如下表所示：
应试者 | 面试成绩 | 笔试成绩 | 才艺 |
甲 | 83 | 79 | 90 |
乙 | 85 | 80 | 75 |
丙 | 80 | 90 | 73 |
（1）根据三项得分的平均分，从高到低确定应聘者的排名顺序；
（2）学校规定：笔试、面试、才艺得分分别不得低于80分、80分、70分，并按照60%、30%、10%的比例计入个人总分，请你说明谁会被录用？
【题目】列方程（组）及不等式（组）解应用题：
水是生命之源.为了鼓励市民节约用水，江夏区水务部门实行居民用水阶梯式计量水价政策；若居民每户每月用水量不超过10立方米，每立方米按现行居民生活用水水价收费（现行居民生活用水水价=基本水价+污水处理费）；若每户每月用水量超过10立方米，则超过部分每立方米在基本水价基础上加价100%，但每立方米污水处理费不变.
下面表格是某居民小区4月份甲、乙两户居民生活用水量及缴纳生活用水水费的情况统计：
4月份居民用水情况统计表
（注：污水处理的立方数=实际生活用水的立方数）
用水量（立方米） | 缴纳生活用水费用（元） | |
甲用户 | 8 | 27.6 |
乙用户 | 12 | 46.3 |
（1）求每立方米的基本水价和每立方米的污水处理费各是多少？
（2）设这个小区某居民用户5月份用水
立方米，需要缴纳的生活用水水费为
元.若他5月份生活用水水费计划不超过64元，该用户5月份最多可用水多少立方米？
