题目内容
【题目】如图，长方形ABCD中，AB=6cm，BC=4cm，点P从点A出发（不含点A），沿A→B→C→D运动，同时，点Q从点B出发（不含点B），沿B→C→D运动，当点P到达点B时，点Q恰好到达点C，已知点P每秒比点Q每秒多运动1cm，当其中一点到达点D（不含点D）时，另一点停止运动．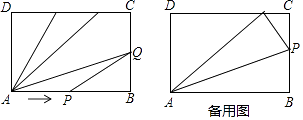
（1）求P、Q两点的速度；
（2）当其中一点到达点D时，另一点距离D点 cm（直接写答案）；
（3）设点P、Q的运动时间为t（x），请用含t的代数式表示△APQ的面积为S（cm3），并写出t的取值范围．
【答案】
（1）
解：∵当点P到达点B时，点Q恰好到达点C，
∴P、Q两点的速度之比为：6：4=3：2，
设点P的速度是3xcm/s，则点Q的速度是2xcm/s，
由题意得，3x﹣2x=1，
解得，x=1，
∴点P的速度是3cm/s，则点Q的速度是2cm/s
（2）1
（3）
解：当0≤t≤2时，AP=3t，BQ=2t，
∴△APQ的面积为S= 
×AP×BQ=3t2，
当2＜t≤ 
时，BP=3t﹣6，CP=10﹣3t，CQ=2t﹣4，QD=10﹣2t，
∴△APQ的面积为S=6×4﹣ ×6×（3t﹣6）﹣ ×4×（10﹣2t）﹣ ×（10﹣3t）×（2t﹣4）=3t2﹣21t+42，
当 ＜t≤5时，PQ=6﹣（3t﹣10）﹣[6﹣（2t﹣4）]=6﹣t，
∴△APQ的面积为S= ×PQ×AD=12﹣2t
【解析】（2）点P到达点D所需的时间为：（6+4+6）÷3= 
s，
点Q到达点D所需的时间为：（6+4）÷2=5s，
∴点Q先到达点D，
则点P距离D点16﹣3×5=1cm，
所以答案是：1；
【考点精析】关于本题考查的等腰直角三角形和翻折变换（折叠问题），需要了解等腰直角三角形是两条直角边相等的直角三角形；等腰直角三角形的两个底角相等且等于45°；折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等才能得出正确答案．
