Question

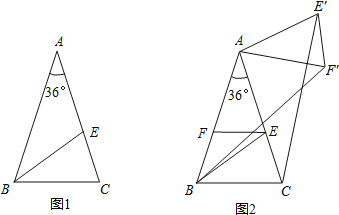
【题目】如图1，在△ABC中，∠A＝36°，AB＝AC，∠ABC的平分线BE交AC于E．

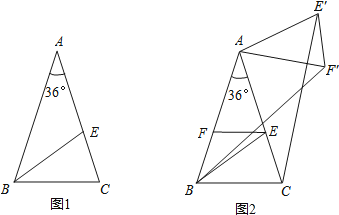
（1）求证：AE＝BC；

（2）如图2，过点E作EF∥BC交AB于F，将△AEF绕点A逆时针旋转角α（0°＜α＜144°）得到△AE′F′，连结CE′、BF′，求证：CE′＝BF′．

Answer 1

【答案】（1）见解析；（2）见解析．

【解析】

（1）根据等腰三角形的性质以及角平分线的性质得出对应角之间的关系进而得出答案；
（2）由旋转的性质可知：∠E′AC＝∠F′AB，AE′＝AF′，根据全等三角形证明方法得出即可；

（1）证明：∵AB＝AC，∠A＝36°，

∴∠ABC＝∠C＝72°，

又∵BE平分∠ABC，

∴∠ABE＝∠CBE＝36°，

∴∠BEC＝180°﹣∠C﹣∠CBE＝72°，

∴∠ABE＝∠A，∠BEC＝∠C，

∴AE＝BE，BE＝BC，

∴AE＝BC．

（2）证明：∵AC＝AB且EF∥BC，

∴AE＝AF；

由旋转的性质可知：，，

∵在△CAE′和△BAF′中

，

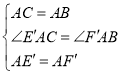∴△CAE′≌△BAF′（SAS），

∴CE′＝BF′．