题目内容
【题目】如图,菱形ABCD中,∠ABC=60°,有一度数为60°的∠MAN绕点A旋转.
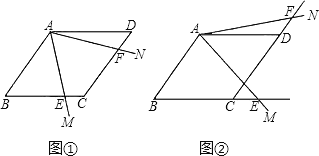
(1)如图①,若∠MAN的两边AM,AN分别交BC,CD于点E,F,则线段CE,DF的大小关系如何?请证明你的结论;
(2)如图②,若∠MAN的两边AM,AN分别交BC,CD的延长线于点E,F,猜想线段CE,DF的大小关系如何?为什么?
【答案】(1)CE=DF(2)CE=DF
【解析】
(1)连接AC,易得△ABC、△ACD为正三角形,根据等边三角形的性质,利用ASA即可判定△AEC≌△AFD,因为全等三角形的对应边相等,所以CE=DF.
(2)结论CE=DF仍然成立,同(1)类似可得△ACE≌△ADF(AAS),从而求得结论.
(1)猜想:CE=DF.
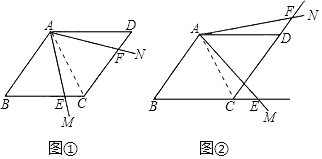
如图①,连接AC,
∵菱形ABCD中,∠ABC=60°,
∴△ABC、△ACD为正三角形.
∵AC=AD,∠ACE=∠ADF=60°,∠CAE=∠DAF=60°-∠CAF,
∴△AEC≌△AFD(ASA).
∴CE=DF.
(2)CE=DF,
如图②,连接AC,
∵菱形ABCD中,∠ABC=60°,
∴△ABC、△ACD为正三角形.
∵AC=AD,∠ACB=∠ADC=60°,
∴∠ACE=∠ADF=120°.
∵∠CAE=∠DAF=60°-∠DAE,
∴△ACE≌△ADF(AAS).
∴CE=DF.

练习册系列答案
相关题目