题目内容
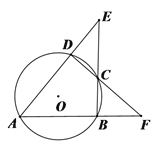
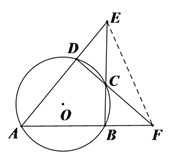
【题目】如图,⊙O的内接四边形ABCD两组对边的延长线分别交于点E,F.
(1)若∠E=∠F时,求证:∠ADC=∠ABC;
(2)若∠E=∠F=42°时,求∠A的度数;
(3)若∠E= ![]() ,∠F=
,∠F= ![]() ,且
,且![]() ≠
≠![]() .请你用含有
.请你用含有![]() 、
、![]() 的代数式表示∠A的大小.
的代数式表示∠A的大小.
【答案】(1)证明见解析;(2)48°;(3)![]()
【解析】(1)由三角形的内角和为180度可知:
∠E+∠A +∠ABC =180°,∠F+∠A +∠ADC =180°,
∵∠E=∠F,∴∠ADC=∠ABC;
(2)由(1)可得∠ADC=∠ABC,
而四边形ABCD为⊙O的内接四边形,
故∠ADC+∠ABC=180°,即∠ADC=∠ABC=90°,
∴∠A =48°;
(3)如图,连结EF,根据圆内接四边形的性质
得∠ECD=∠A,再根据三角形外角性质
得∠ECD=∠CEF+∠CFE,则∠A=∠CEF+∠CFE,
然后根据三角形内角和定理
有∠A+∠CEF+∠CFE+∠AEB+∠AFD=180°,
即2∠A+ ![]() +
+ ![]() =180°,再解方程即可得:
=180°,再解方程即可得: ![]() .
.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
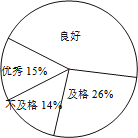
【题目】为了解某市初三学生的体育测试成绩和课外体育锻炼时间的情况,现从全市初三学生体育测试成绩中随机抽取200名学生的体育测试成绩作为样本.体育成绩分为四个等次:优秀、良好、及格、不及格.
体育锻炼时间 | 人数 |
4≤x≤6 |
|
2≤x<4 | 43 |
0≤x<2 | 15 |
(1)试求样本扇形图中体育成绩“良好”所对扇形圆心角的度数;
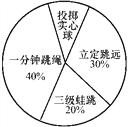
(2)统计样本中体育成绩“优秀”和“良好”学生课外体育锻炼时间表(如图表所示),请将图表填写完整(记学生课外体育锻炼时间为x小时);
(3)全市初三学生中有14400人的体育测试成绩为“优秀”和“良好”,请估计这些学生中课外体育锻炼时间不少于4小时的学生人数.