题目内容
【题目】如图,Rt△ABC,∠BAC=90°,点D,E分别为边AB,BC的中点,点F在CA延长线上,且∠FDA=∠B.
(1)求证:AF=DE;
(2)若AC=3,BC=5,求四边形AEDF的周长.
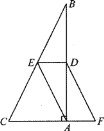
【答案】(1)见解析;(2)8
【解析】
(1)根据中位线的性质可知DE∥CF,再根据直角三角形斜边上的中线等于斜边的一半可得AE=BE,进而推出∠BAE=∠B=∠FDA,推出AE∥DF,然后根据平行四边形的判定和性质得出结论;
(2)由平行四边形的性质可知AF=ED,AE=DF,根据中位线的性质可知ED=![]() AC,再根据直角三角形斜边上的中线等于斜边的一半可得AE=BE=
AC,再根据直角三角形斜边上的中线等于斜边的一半可得AE=BE=![]() BC,根据平行四边形的周长=2DE+2AE即可求出答案.
BC,根据平行四边形的周长=2DE+2AE即可求出答案.
解:∵Rt△ABC,∠BAC=90°,点D,E分别为边AB,BC的中点,
∴ED∥AC,AE=BE,
∴∠BAE=∠B
∵∠B=∠FDA,
∴∠BAE =∠FDA,
∴AE∥DF,
∴四边形AEDF是平行四边形,
∴AF=DE;
(2)∵四边形AEDF是平行四边形,
∴ED=AF
∵Rt△ABC,∠BAC=90°,点D,E分别为边AB,BC的中点,
∴ED=![]() AC,AE=BE=
AC,AE=BE=![]() BC,
BC,
∵AC=3,BC=5,
∴平行四边形AEDF的周长=2DE+2AE=AC+BC=3+5=8

练习册系列答案
相关题目
【题目】下表是二次函数y=ax2+bx+c的部分x,y的对应值:
x | … | -1 | - | 0 |
| 1 |
| 2 |
| 3 | … |
y | … | 2 |
| -1 | - | -2 | - | -1 |
| 2 | … |
(1)此二次函数图象的顶点坐标是 ;
(2)当抛物线y=ax2+bx+c的顶点在直线y=x+n的下方时,n的取值范围是 。