题目内容
如图,∠AOB中,OD是∠BOC的平分线,OE是∠AOC的平分线,若∠AOB=140,则∠EOD=___________度.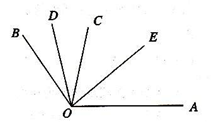

70
由图形可知∠DOE=∠DOC+∠EOC,然后根据角平分线的性质,可推出∠DOC= 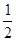 ∠BOC,∠EOC=
∠BOC,∠EOC= 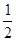 ∠AOC,由此可推出∠DOE=
∠AOC,由此可推出∠DOE= 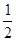 ∠AOB,最后根据∠AOB的度数,即可求出结论.
∠AOB,最后根据∠AOB的度数,即可求出结论.
解:∵OD是∠BOC的平分线,OE是∠AOC的平分线,
∴∠DOC=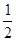 ∠BOC,∠EOC=
∠BOC,∠EOC=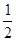 ∠AOC,
∠AOC,
∴∠DOE=∠DOC+∠EOC=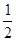 ∠AOB,
∠AOB,
∵∠AOB=140°,
∴∠EOD=70°.
故答案为70.
本题主要考查角平分线的性质,关键在于运用数形结合的思想推出∠DOE=∠DOC+∠EOC=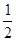 ∠AOB.
∠AOB.
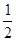 ∠BOC,∠EOC=
∠BOC,∠EOC= 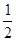 ∠AOC,由此可推出∠DOE=
∠AOC,由此可推出∠DOE= 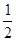 ∠AOB,最后根据∠AOB的度数,即可求出结论.
∠AOB,最后根据∠AOB的度数,即可求出结论.解:∵OD是∠BOC的平分线,OE是∠AOC的平分线,
∴∠DOC=
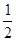 ∠BOC,∠EOC=
∠BOC,∠EOC=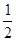 ∠AOC,
∠AOC,∴∠DOE=∠DOC+∠EOC=
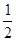 ∠AOB,
∠AOB,∵∠AOB=140°,
∴∠EOD=70°.
故答案为70.
本题主要考查角平分线的性质,关键在于运用数形结合的思想推出∠DOE=∠DOC+∠EOC=
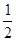 ∠AOB.
∠AOB.
练习册系列答案
相关题目
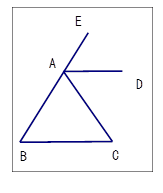
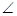 EAD=
EAD=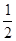
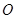 在直线PQ上,
在直线PQ上,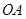 是
是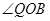 的平分线,
的平分线,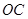 是
是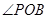 的平分线,那么下列说法错误的是( )
的平分线,那么下列说法错误的是( )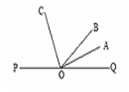
 与
与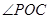 互余
互余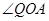 互余
互余 与
与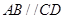 ,
,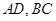 相交于点
相交于点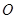 ,
,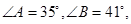 则
则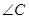 的度数是……………………………………………………………………………( )
的度数是……………………………………………………………………………( )