题目内容
如图，线段AB、 AC的中垂线交于点D，且∠A=130°， 则∠BDC的度数为( )
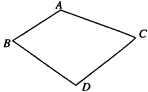
A．90° B．100° C．120° D．130°
A．90° B．100° C．120° D．130°
B
过D点作DE⊥AB，DF⊥AC，连接AD，
∴线段DE、DF分别是线段AB、AC的中垂线，
∴∠AED=∠AFD=90°，则∠AED+∠AFD=180°
∵∠A=130°，
∴∠EDF=50°，∠ADE=∠ADF=25°
∵线段DE、DF分别是线段AB、AC的中垂线，
∴△AED≌△BED，△AFD≌△CFD，
∴∠BDE=∠EDA=25°，∠ADF=∠CDF=25°，
∴∠BDC=50+25+25=100°．
故选B．
∴线段DE、DF分别是线段AB、AC的中垂线，
∴∠AED=∠AFD=90°，则∠AED+∠AFD=180°
∵∠A=130°，
∴∠EDF=50°，∠ADE=∠ADF=25°
∵线段DE、DF分别是线段AB、AC的中垂线，
∴△AED≌△BED，△AFD≌△CFD，
∴∠BDE=∠EDA=25°，∠ADF=∠CDF=25°，
∴∠BDC=50+25+25=100°．
故选B．
练习册系列答案
相关题目
∥
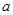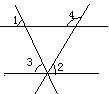
，∠1=110°，∠2=150°，则∠3=______°．
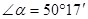，则它的余角等于________；
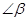的补角是
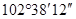，则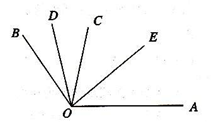
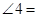
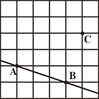
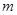的房屋后墙，围一块150
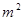的矩形养鸡场，现在有篱笆共35