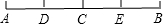题目内容
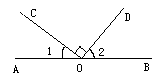
如图所示,点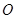 在直线PQ上,
在直线PQ上,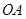 是
是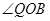 的平分线,
的平分线,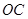 是
是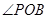 的平分线,那么下列说法错误的是( )
的平分线,那么下列说法错误的是( )
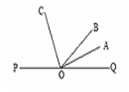
 在直线PQ上,
在直线PQ上,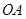 是
是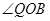 的平分线,
的平分线,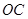 是
是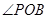 的平分线,那么下列说法错误的是( )
的平分线,那么下列说法错误的是( )
A. 与 与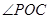 互余 互余 | B.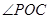 与 与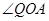 互余 互余 |
C.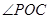 与 与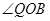 互补 互补 | D. 与 与 互补 互补 |
C
根据角平分线的定义可得∠QOA=∠AOB= 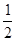 ∠BOQ,∠POC=∠BOC=
∠BOQ,∠POC=∠BOC= 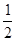 ∠POB,然后根据互为余角的两个角的和等于90°,互为补角的两个角的和等于180°对各选项分析判断后利用排除法求解.
∠POB,然后根据互为余角的两个角的和等于90°,互为补角的两个角的和等于180°对各选项分析判断后利用排除法求解.
解:∵OA是∠QOB的平分线,
∴∠QOA=∠AOB=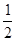 ∠BOQ,
∠BOQ,
∵OC是∠POB的平分线,
∴∠POC=∠BOC=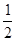 ∠POB,
∠POB,
∵点O在直线PQ上,
∴∠BOQ+∠POB=180°,
A、∠AOB+∠POC=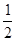 (∠BOQ+∠POB)=
(∠BOQ+∠POB)=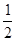 ×180°=90°,
×180°=90°,
所以,∠AOB与∠POC互余,说法正确,故本选项错误;
B、∠POC+∠QOA=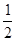 (∠BOQ+∠POB)=
(∠BOQ+∠POB)=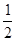 ×180°=90°,
×180°=90°,
所以,∠POC与∠QOA互余,说法正确,故本选项错误;
C、∠POC+∠QOB=180°-∠BOC≠180°,
所以,∠POC与∠QOB不互补,说法错误,故本选项正确;
D、∠AOP+∠AOB=∠AOP+∠AOQ=180°,
所以,∠AOP与∠AOB互补,说法正确,故本选项错误.
故选C.
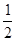 ∠BOQ,∠POC=∠BOC=
∠BOQ,∠POC=∠BOC= 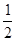 ∠POB,然后根据互为余角的两个角的和等于90°,互为补角的两个角的和等于180°对各选项分析判断后利用排除法求解.
∠POB,然后根据互为余角的两个角的和等于90°,互为补角的两个角的和等于180°对各选项分析判断后利用排除法求解.解:∵OA是∠QOB的平分线,
∴∠QOA=∠AOB=
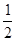 ∠BOQ,
∠BOQ,∵OC是∠POB的平分线,
∴∠POC=∠BOC=
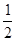 ∠POB,
∠POB,∵点O在直线PQ上,
∴∠BOQ+∠POB=180°,
A、∠AOB+∠POC=
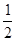 (∠BOQ+∠POB)=
(∠BOQ+∠POB)=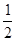 ×180°=90°,
×180°=90°,所以,∠AOB与∠POC互余,说法正确,故本选项错误;
B、∠POC+∠QOA=
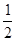 (∠BOQ+∠POB)=
(∠BOQ+∠POB)=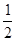 ×180°=90°,
×180°=90°,所以,∠POC与∠QOA互余,说法正确,故本选项错误;
C、∠POC+∠QOB=180°-∠BOC≠180°,
所以,∠POC与∠QOB不互补,说法错误,故本选项正确;
D、∠AOP+∠AOB=∠AOP+∠AOQ=180°,
所以,∠AOP与∠AOB互补,说法正确,故本选项错误.
故选C.

练习册系列答案
相关题目
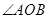 互补的角为( )
互补的角为( )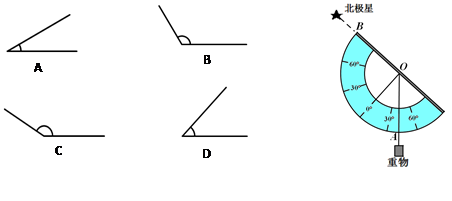
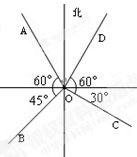
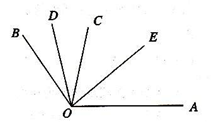
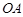 的方向是北偏西
的方向是北偏西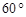
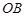 的方向是西南方向
的方向是西南方向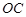 的方向是南偏东
的方向是南偏东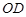 的方向是北偏东
的方向是北偏东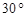
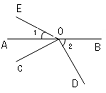
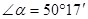 ,则它的余角等于________;
,则它的余角等于________;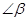 的补角是
的补角是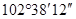 ,则
,则