题目内容
【题目】如图,四边形ABCD中,AD∥BC,∠ADC=α,P为直线CD上一动点,点M在线段BC上,连MP,∠MPD=β 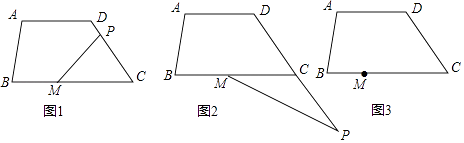
(1)如图,若MP⊥CD,α=120°,则∠BMP=;
(2)如图,当P点在DC延长线上时,∠BMP=;
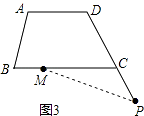
(3)如图,当P点在CD延长线上时,请画出图形,写出∠BMP、β、α之间的数量关系,并证明你的结论.
【答案】
(1)150°
(2)60°+β
(3)解:∵AD∥BC,
∴∠BCP=∠ADC=α,
在△CMP中,∠CMP=180°﹣∠BCP﹣∠MPD=180°﹣α﹣β,
∴∠BMP=180°﹣∠CMP=180°﹣(60°﹣α)=α+β.
【解析】解:(1)∵AD∥BC, ∴∠C=180°﹣∠ADC=180°﹣120°=60°,
∵MP⊥CD,
∴∠CMP=90°﹣∠C=90°﹣60°=30°,
∴∠BMP=180°﹣∠CMP=180°﹣30°=150°;(2)∵AD∥BC,
∴∠C=180°﹣∠ADC=180°﹣120°=60°,
在△CMP中,∠CMP=180°﹣∠C﹣∠MPD=180°﹣60°﹣β=120°﹣β,
∴∠BMP=180°﹣∠CMP=180°﹣(120°﹣β)=60°+β;
所以答案是:(1)150°;(2)60°+β;
【考点精析】根据题目的已知条件,利用平行线的性质的相关知识可以得到问题的答案,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目