题目内容
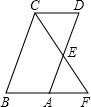 如图,已知?ABCD中,E为AD的中点,CE的延长线交BA的延长线于点F.则下列结论中不正确的是
如图,已知?ABCD中,E为AD的中点,CE的延长线交BA的延长线于点F.则下列结论中不正确的是
- A.S△BCF=4S△CDE
- B.∠B=∠D
- C.CD=FA
- D.∠F=∠BCF
D
分析:过C作CH⊥AD于H,推出∠D=∠DAF,∠DCE=∠F,证△DCE≌△AFE,推出△BCF的面积等于平行四边形面积,即为AD×CH,而△CDE的面积为 ×
× AD×CH,即可判断A;根据平行四边形性质即可判断B;由△DCE≌△AFE,推出CD=AF,即可判断C;推出∠DCE=∠F,即可判断D.
AD×CH,即可判断A;根据平行四边形性质即可判断B;由△DCE≌△AFE,推出CD=AF,即可判断C;推出∠DCE=∠F,即可判断D.
解答:A、过C作CH⊥AD于H,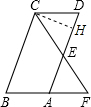
∵四边形ABCD是平行四边形,
∴CD∥AB,
∴∠D=∠DAF,∠DCE=∠F,
∵在△DCE和△AFE中
 ,
,
∴△DCE≌△AFE,
∴S△DEC=S△AEF= DE×CH=
DE×CH= ×
× AD×CH,
AD×CH,
∵S△BCF=S四边形ABCE+S△AEF,
=S四边形ABCE+S△DEC,
=S平行四边形ABCD,
=AD×CH,
∴S△BCF=4S△CDE,故本选项错误;
B、∵四边形ABCD是平行四边形,
∴∠B=∠D,故本选项错误;
C、∵△DCE≌△AFE,
∴CD=AF,故本选项错误;
D、∵△DCE≌≌△AFE,
∴∠F=∠DCF,
已知没有告诉(也不能推出)∠DCE=∠BCF,故本选项正确;
故选D.
点评:本题考查的知识点是平行四边形的性质、全等三角形性质和判定,平行线的性质,主要培养学生运用性质进行推理的能力,题目比较好,难度适中.
分析:过C作CH⊥AD于H,推出∠D=∠DAF,∠DCE=∠F,证△DCE≌△AFE,推出△BCF的面积等于平行四边形面积,即为AD×CH,而△CDE的面积为
 ×
× AD×CH,即可判断A;根据平行四边形性质即可判断B;由△DCE≌△AFE,推出CD=AF,即可判断C;推出∠DCE=∠F,即可判断D.
AD×CH,即可判断A;根据平行四边形性质即可判断B;由△DCE≌△AFE,推出CD=AF,即可判断C;推出∠DCE=∠F,即可判断D.解答:A、过C作CH⊥AD于H,

∵四边形ABCD是平行四边形,
∴CD∥AB,
∴∠D=∠DAF,∠DCE=∠F,
∵在△DCE和△AFE中
 ,
,∴△DCE≌△AFE,
∴S△DEC=S△AEF=
 DE×CH=
DE×CH= ×
× AD×CH,
AD×CH,∵S△BCF=S四边形ABCE+S△AEF,
=S四边形ABCE+S△DEC,
=S平行四边形ABCD,
=AD×CH,
∴S△BCF=4S△CDE,故本选项错误;
B、∵四边形ABCD是平行四边形,
∴∠B=∠D,故本选项错误;
C、∵△DCE≌△AFE,
∴CD=AF,故本选项错误;
D、∵△DCE≌≌△AFE,
∴∠F=∠DCF,
已知没有告诉(也不能推出)∠DCE=∠BCF,故本选项正确;
故选D.
点评:本题考查的知识点是平行四边形的性质、全等三角形性质和判定,平行线的性质,主要培养学生运用性质进行推理的能力,题目比较好,难度适中.

练习册系列答案
相关题目
 14、如图,已知?ABCD中,AB=4,BC=6,BC边上的高AE=2,则DC边上的高AF的长是
14、如图,已知?ABCD中,AB=4,BC=6,BC边上的高AE=2,则DC边上的高AF的长是

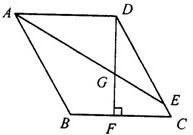 26、如图,已知?ABCD,AE平分∠BAD,交DC于E,DF⊥BC于F,交AE于G,且DF=AD.
26、如图,已知?ABCD,AE平分∠BAD,交DC于E,DF⊥BC于F,交AE于G,且DF=AD.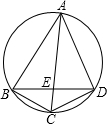 如图,已知ABCD是圆的内接四边形,对角线AC和BD相交于E,BC=CD=4,AE=6,如果线段BE和DE的长都是整数,则BD的长等于
如图,已知ABCD是圆的内接四边形,对角线AC和BD相交于E,BC=CD=4,AE=6,如果线段BE和DE的长都是整数,则BD的长等于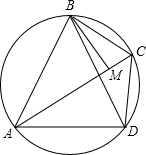 如图,已知ABCD是圆O的内接四边形,AB=BD,BM⊥AC于M,求证:AM=DC+CM.
如图,已知ABCD是圆O的内接四边形,AB=BD,BM⊥AC于M,求证:AM=DC+CM.