题目内容
14、如图，已知?ABCD中，AB=4，BC=6，BC边上的高AE=2，则DC边上的高AF的长是3
．分析：根据平行四边形的对边相等，可得CD=AB=6，又因为S?ABCD=BC•AE=CD•AF，所以求得DC边上的高AF的长是3．
解答：解：∵四边形ABCD是平行四边形，
∴BC=AD=6，
∴S?ABCD=BC•AE=CD•AF=6×2=12，
∴AF=3．
∴DC边上的高AF的长是3．
故答案为3．
∴BC=AD=6，
∴S?ABCD=BC•AE=CD•AF=6×2=12，
∴AF=3．
∴DC边上的高AF的长是3．
故答案为3．
点评：此题考查了平行四边形的性质：平行四边形的对边相等．还要注意平行四边形的面积的求解方法：底乘以高．
练习册系列答案
阅读快车系列答案
相关题目
26、如图，已知?ABCD，AE平分∠BAD，交DC于E，DF⊥BC于F，交AE于G，且DF=AD．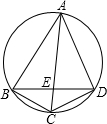
如图，已知ABCD是圆的内接四边形，对角线AC和BD相交于E，BC=CD=4，AE=6，如果线段BE和DE的长都是整数，则BD的长等于
如图，已知ABCD是圆O的内接四边形，AB=BD，BM⊥AC于M，求证：AM=DC+CM．