题目内容
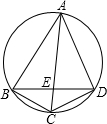 如图,已知ABCD是圆的内接四边形,对角线AC和BD相交于E,BC=CD=4,AE=6,如果线段BE和DE的长都是整数,则BD的长等于
如图,已知ABCD是圆的内接四边形,对角线AC和BD相交于E,BC=CD=4,AE=6,如果线段BE和DE的长都是整数,则BD的长等于分析:已知了BC=CD,可得出弧BC=弧CD,根据圆周角定理可得出∠BAC=∠CBD;易证得△CBE∽△CAB,根据所得的关于AC、CE、BC的比例关系式可求出EC的长;
根据相交弦定理得AE•EC=BE•ED,又已知BE、DE的长是整数,可求出BE、DE的取值情况;然后在△BCD中,根据三角形三边关系定理将不合题意的解舍去.
根据相交弦定理得AE•EC=BE•ED,又已知BE、DE的长是整数,可求出BE、DE的取值情况;然后在△BCD中,根据三角形三边关系定理将不合题意的解舍去.
解答:解:∵BC=CD=4,
∴
=
;
∴∠CBE=∠CDB=∠CAB;
又∵∠BCE=∠ACB,
∴△CBE∽△CAB,得
=
,即
=
;
化简得:EC2+6EC-16=0,解得:EC=2(负值舍去).
由相交弦定理,得:BE•ED=AE•EC,
∴BE•ED=2×6=12;
则BE和DE可取的值分别为3,4;2,6;1,12;
又因为BC=CD=4,所以BD<BC+CD=4+4=8.
故为BD=3+4=7.
∴
 |
| BC |
 |
| CD |
∴∠CBE=∠CDB=∠CAB;
又∵∠BCE=∠ACB,
∴△CBE∽△CAB,得
| BC |
| AC |
| EC |
| BC |
| 4 |
| 6+EC |
| EC |
| 4 |
化简得:EC2+6EC-16=0,解得:EC=2(负值舍去).
由相交弦定理,得:BE•ED=AE•EC,
∴BE•ED=2×6=12;
则BE和DE可取的值分别为3,4;2,6;1,12;
又因为BC=CD=4,所以BD<BC+CD=4+4=8.
故为BD=3+4=7.
点评:此题是一道开放题,先根据相似三角形的性质和相交弦定理估算出BE、ED,再根据三角形两边之和大于第三边将不合题意的解舍去,综合性较强,难度较大.

练习册系列答案
相关题目
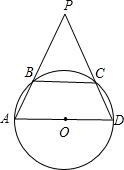 如图,已知ABCD是一个以AD为直径的圆内接四边形,分别延长AB和DC,它们相交于P,若∠APD=60°,AB=5,PC=4,则⊙O的面积为( )
如图,已知ABCD是一个以AD为直径的圆内接四边形,分别延长AB和DC,它们相交于P,若∠APD=60°,AB=5,PC=4,则⊙O的面积为( )| A、25π | B、16π | C、15π | D、13π |
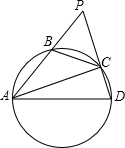 如图,已知ABCD是一个半径为R的圆内接四边形,AB=12,CD=6,分别延长AB和DC,它们相交于点P,且BP=8,∠APD=60°,则R=
如图,已知ABCD是一个半径为R的圆内接四边形,AB=12,CD=6,分别延长AB和DC,它们相交于点P,且BP=8,∠APD=60°,则R=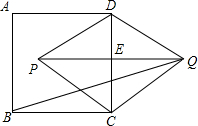 如图,已知ABCD是正方形,以CD为一边向CD两旁作等边三角形PCD和等边三角形QCD,那么tan∠PQB的值为
如图,已知ABCD是正方形,以CD为一边向CD两旁作等边三角形PCD和等边三角形QCD,那么tan∠PQB的值为 如图,已知ABCD是圆O的内接四边形,AB=BD,BM⊥AC于M,求证:AM=DC+CM.
如图,已知ABCD是圆O的内接四边形,AB=BD,BM⊥AC于M,求证:AM=DC+CM.