题目内容
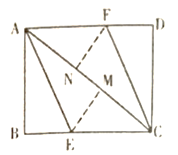
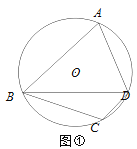
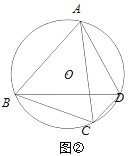
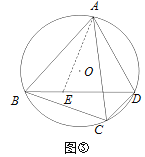
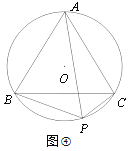
【题目】如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠AFC,以下结论:①AD∥BC;②∠ACB=2∠ADB;③∠ADC=90°—∠ABD;④∠BDC=![]() ∠BAC,其中正确的结论有_____________。
∠BAC,其中正确的结论有_____________。

【答案】①②③④
【解析】
根据角平分线定义得出∠ABC=2∠ABD=2∠DBC,∠EAC=2∠EAD,∠ACF=2∠DCF,根据三角形的内角和定理得出∠BAC+∠ABC+∠ACB=180°,根据三角形外角性质得出∠ACF=∠ABC+∠BAC,∠EAC=∠ABC+∠ACB,根据已知结论逐步推理,即可判断各项.
解:∵AD平分∠EAC,
∴∠EAC=2∠EAD,
∵∠EAC=∠ABC+∠ACB,∠ABC=∠ACB,
∴∠EAD=∠ABC,
∴AD∥BC,∴①正确;
∵AD∥BC,
∴∠ADB=∠DBC,
∵BD平分∠ABC,∠ABC=∠ACB,
∴∠ABC=∠ACB=2∠DBC,
∴∠ACB=2∠ADB,∴②正确;
∵AD平分∠EAC,CD平分∠ACF,
∴∠DAC=![]() ∠EAC,∠DCA=
∠EAC,∠DCA=![]() ∠ACF,
∠ACF,
∵∠EAC=∠ABC+∠ACB,∠ACF=∠ABC+∠BAC,∠ABC+∠ACB+∠BAC=180°,
∴∠ADC=180°(∠DAC+∠ACD)
=180°![]() (∠EAC+∠ACF)
(∠EAC+∠ACF)
=180°![]() (∠ABC+∠ACB+∠ABC+∠BAC)
(∠ABC+∠ACB+∠ABC+∠BAC)
=180°![]() (180°+∠ABC)
(180°+∠ABC)
=90°![]() ∠ABC
∠ABC
=90°—∠ABD,∴③正确;
∵∠ACF=2∠DCF,∠ACF=∠BAC+∠ABC,∠ABC=2∠DBC,∠DCF=∠DBC+∠BDC,
∴∠BAC=2∠BDC,∴④正确,
故答案为:①②③④.

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案【题目】将一些数排列成下表中的四列:
第1列 | 第2列 | 第3列 | 第4列 | |
第1行 | 1 | 4 | 5 | 10 |
第2行 | 4 | 8 | 10 | 12 |
第3行 | 9 | 12 | 15 | 14 |
… | … | … | … | … |
(1)第4行第1列的数是多少?直接写出答案;
(2)第17行的四个数之和是多少?请写出适当的过程;
(3)数100所在的行和列分别是多少?直接写出答案.