Question

【题目】下图是行列间隔都为1个单位的点阵：
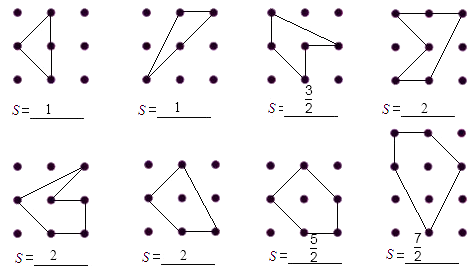
（1）你能计算点阵中多边形的面积吗？请将答案直接填入图中横线上．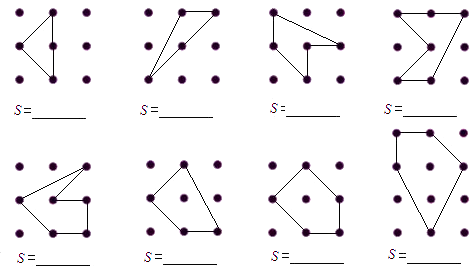

（2）若用a表示多边形内部的点数，b表示多边形边界上的点数，S表示多边形的面积，你能用含a和b的代数式表示S=；
（3）请你利用（2）中的公式来求a=4，b=20时，多边形的面积S．

Answer 1

【答案】
（1）

（2）
（3）

解：

【解析】解：（1）因为点阵中行列间隔都为1个单位，
所以，第一个多边形的面积为1=0+ ×4﹣1；
第二个多边形的面积为1=0+ ×4﹣1；
第三个多边形的面积为 =0+ ×5﹣1；
第四个多边形的面积为2=0+ ×6﹣1；
第五个多边形的面积为2=0+ ×6﹣1；
第六个多边形的面积为2=1+ ×4﹣1；
第七个多边形的面积为 =1+ ×5﹣1；
第三个多边形的面积为 =2+ ×5﹣1；
通过计算，并对上述结果进行归纳总结可以发现：
等号左边的数为多边形的面积，等号右边的第一个数是多边形内部的点数，第二个和第四个数都是常数，
第三个数是多边形边界上的点数．
所以说多边形的面积等于多边形内部的点数加上 与多边形边界上的点数的乘积然后减去1．

2）若用a表示多边形内部的点数，b表示多边形边界上的点数，S表示多边形的面积，按照（1）中总结的规律，则有：s= ．