Question

【题目】数形结合是重要的数学思想方法之一，数形结合具体地说就是将抽象数学语言与直观图形结合起来，使抽象思维与形象思维结合起来，通过“数”与“形”之间的对应和转变来解决数学问题。数轴是数形结合的最基础图形，是连接数与形的桥梁之一，请解决下面的问题：

（1）如图1，点B表示的数是1，则点A表示的数是 .

（2）如果点M表示数－2，将点M向右移动6个单位长度到达终点N，那么终点N表示的数是4，此时M、N两点间的距离是 .

（3）若∣x－0∣意义表示数x到原点的距离，则∣x－3∣的意义表示数x到3的距离；类似的式子∣x＋3∣=4，则x= .

（4）由（3）可知，一般地，如果点A表示数为a，点B表示的数b，则A、B两点间的距离表示为 .

（5）如图2，数轴上的两个点A、B所表示的数分别是a，b，点O为原点。在a＋b，a－b，∣a∣－∣b∣这三个运算结果中，是正数的有 个.

（6）利用数轴直接写出∣x－2∣＋∣x＋5∣的最小值= .

Answer 1

【答案】（1）-3；（2）6；（3）x=-7或x=1；（4）|a-b|；（5）1；(6)7.

【解析】

（1）直接观察数轴即可得答案；

（2）M平移了6个单位，则MN=6；

（3）∣x＋3∣=4表示x到-3的距离为4，在数轴上即可发现答案；

（4）根据两数差的绝对值表示距离，即可完成解答;

（5）由数轴可以发现b＜0，a＞0，|b|＞|a|，即可确定它们的正负;

（6）∣x－2∣＋∣x＋5∣最小值表示即x到2和x到-5的距离之和，通过数轴即可得出结果

解：（1）直接观察数轴即可得到，A表示的数为-3;
（2）在数轴上平移6个单位，即MN=6，故答案为：6；

（3） ∣x＋3∣=4表示x到-3的距离为4，即x=-7或x=1，故答案为：x=-7或x=1；

（4）A、B两点间的距离表示为|a-b|，故答案为：|a-b|

（5）由数轴可以发现b＜0，a＞0，|b|＞|a|，

则a＋b＜0，a-b＞0，∣a∣－∣b∣＜0，故答案为1.

（6）如图：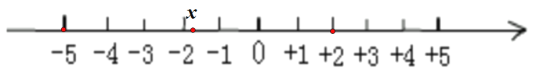

可以，发现当-5＜x＜2时，x到2和x到-5的距离之和均为7，不在这个范围大于7，所以∣x－2∣＋∣x＋5∣的最小值为7.