题目内容
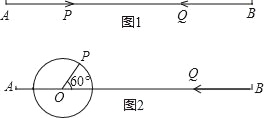
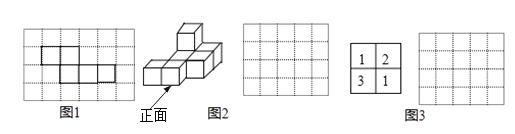
【题目】(1)小明准备制作一个封闭的正方体盒子,他先用5个大小一样的正方形制成如图1所示的拼接图形(实线部分),经折叠后发现还少一个面,请在图中的拼接图形上再接一个正方形,使新拼接的图形经过折叠后能成为一个封闭的正方体盒子.(添加的正方形用阴影表示.只要画出一种即可)
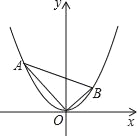
(2)如图2所示的几何体是由几个相同的正方体搭成的,请画出它从正面看的形状图.
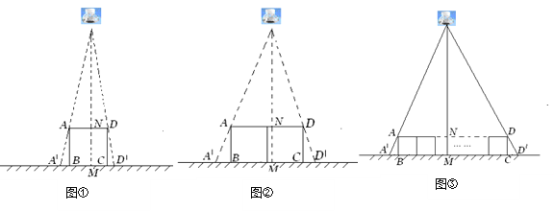
(3)如图3是几个正方体所组成的几何体从上面看的形状图,小正方形中的数字表示该位置小正方体的个数,请画出这个几何体从左面看的形状图.
【答案】(1)见解析;(2)见解析;(3)见解析
【解析】
(1)在第二行3个正方形的下方的任意一个位置添加一个正方形可经过折叠后能成为一个封闭的正方体盒子;
(2)由图可知,主视图有3列,每列小正方数形数目分别为1,2,1,据此可画出图形;
(3)由图可知,左视图有2列,每列小正方形数目分别为2,3,据此可画出图形.
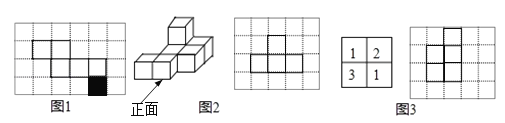
(1)如图1所示:
(2)如图2所示:
(3)如图3所示:

【题目】2019年7月9日,北京市滴滴快车调整了价格,规定车费由“总里程费+总时长费”两部分构成,具体收费标准如下表:(注:如果车费不足起步价,则按起步价收费.)
时间段 | 里程费(元/千米) | 时长费(元/分钟) | 起步价(元) |
06:00—10:00 | 1.80 | 0.80 | 14.00 |
10:00—17:00 | 1.45 | 0.40 | 13.00 |
17:00—21:00 | 1.50 | 0.80 | 14.00 |
21:00—06:00 | 2.15 | 0.80 | 14.00 |
(1)小明07:10乘快车上学,行驶里程6千米,时长10分钟,应付车费 元;
(2)小芳17:20乘快车回家,行驶里程1千米,时长15分钟,应付车费 元;
(3)小华晚自习后乘快车回家,20:45在学校上车.由于道路施工,车辆行驶缓慢,15分钟后选择另外道路,改道后速度是改道前速度的3倍,10分钟后到家,共付了车费37.4元,问从学校到小华家快车行驶了多少千米?