题目内容
【题目】已知二次函数y=x2+bx+c的图象过点(4,3)、(3,0).
(1)求b、c的值;
(2)求出该二次函数图象的顶点坐标和对称轴;
(3)在下图中作出此二次函数的图象,根据图象说明,当x取何值时,y<0?

【答案】(1)b=﹣4,c=3;(2)顶点坐标 为(2,﹣1),对称轴为直线x=2.(3)见解析
【解析】
试题分析:(1)利用待定系数法确定二次函数解析式即可,
(2)将抛物线y=x2﹣4x+3配方,即可得出二次函数图象的顶点坐标和对称轴;
(3)先画出二次函数的图象,由图象可得当1<x<3时,y<0.
解:(1)∵二次函数y=x2+bx+c的图象过点(4,3)、(3,0),
∴![]() ,解得b=﹣4,c=3.
,解得b=﹣4,c=3.
(2)将抛物线y=x2﹣4x+3配方得,y=(x﹣2)2﹣1.
∴顶点坐标 为(2,﹣1),对称轴为直线x=2.
(3)如图,
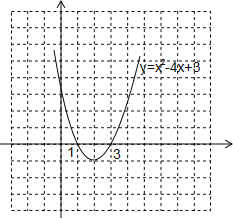
由图象得当1<x<3时,y<0.

【题目】某校从甲、乙两名优秀选手中选一名选手参加全市中学生田径百米比赛.该校预先对这两名选手测试了8次,测试成绩如下表:
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
选手甲的成绩/秒 | 12.1 | 12.2 | 13 | 12.5 | 13.1 | 12.5 | 12.4 | 12.2 |
选手乙的成绩/秒 | 12 | 12.4 | 12.8 | 13 | 12.2 | 12.8 | 12.3 | 12.5 |
根据测试成绩,请你运用所学过的统计知识做出判断,派哪一位选手参加比赛更好?为什么
【题目】某食品公司产销一种食品,已知每月的生产成本y1与产量x之间是一次函数关系,函数y1与自变量z(kg)的部分对应值如下表:
x(单位:kg) | 10 | 20 | 30 |
y1(单位:/元) | 3030 | 3060 | 3090 |
(1)求y1与x之间的函数关系式;
(2)经过试销发现,这种食品每月的销售收入y2(元)与销量x(kg)之间满足如图所示的函数关系
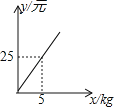
①y2与x之间的函数关系式为 ;
②假设该公司每月生产的该种食品均能全部售出,那么该公司每月至少要生产该种食品多少kg,才不会亏损?
