题目内容
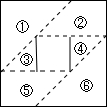
在边长为1的4×4方格上建立直角坐标系(如图甲),在第一象限内画出反比例函数,y=
,y=
,y=
的图象,它们分别经过方格中的一个格点、二个格点、三个格点;在边长为1的10×10方格上建立直角坐标系(如图乙),在第一象限内画出反比例函数的图象,使它们经过方格中的三个或四个格点,则最多可画出( )条.

| 16 |
| x |
| 6 |
| x |
| 4 |
| x |

分析:本题是借用反比例函数要解答一道分解因数的数学问题,要求函数图象要经过3至4个格点,且积不超过100,且为合数,而在解答的过程发现,经过3至4个且横纵坐标不超过10的合数,就将范围缩小到1-40的合数,在这中间去寻找符合条件的数就可以了.
解答:解:由题意知,要使y=
的k为1-100的合数,而这些合数分解质因数后作为横纵坐标的两个数不超过10,
通过实验法得k≤40的合数,这其中只有27个数,
将这27个数进行分解因数后符合条件的k值有:4、6、8、9、10、12、16、18、20、24、30、36、40.共13个.
∴最多可以画13条.
故选B.
| k |
| x |
通过实验法得k≤40的合数,这其中只有27个数,
将这27个数进行分解因数后符合条件的k值有:4、6、8、9、10、12、16、18、20、24、30、36、40.共13个.
∴最多可以画13条.
故选B.
点评:本题考查的是一道反比例函数的综合试题,它涉及到了代数的合数和分解因数,反比例函数的性质.是一道综合性较强的试题,在解答中需要用到实验法.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
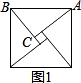
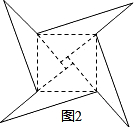
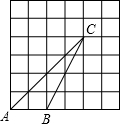
 3、图中的小方格式边长为1的正方形,则在图中一共可以数出正方形的个数是( )
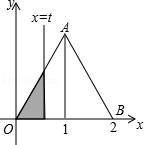
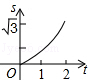
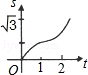
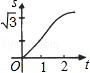
3、图中的小方格式边长为1的正方形,则在图中一共可以数出正方形的个数是( ) 如下图,在直角坐标系的第一象限内,△AOB是边长为2的等边三角形,设直线l:x=t(0≤t≤2)截这个三角形所得位于直线左侧的图形(阴影部分)的面积为f(t),则函数s=f(t)的图象只可能是t大于等于0小于等于1时,函数为Y=3根号x方除以2 图线不应为直线( )
如下图,在直角坐标系的第一象限内,△AOB是边长为2的等边三角形,设直线l:x=t(0≤t≤2)截这个三角形所得位于直线左侧的图形(阴影部分)的面积为f(t),则函数s=f(t)的图象只可能是t大于等于0小于等于1时,函数为Y=3根号x方除以2 图线不应为直线( )